OlliW's Bastelseiten » Field Oriented Control: To FOC or not to FOC

Brushless motors have become a commodity also to hobbyists, and with that modern motor drive technologies crept into their field of vision. Field-oriented control (FOC) is one of these technologies, but is still rarely used in the hobby world. The web provides us with endless articles nicely explaining the FOC algorithm in detail. However, I found them all to present FOC in essentially one and the same way, and in a way which I didn’t found very suitable to answer those questions I was most interested in, such as „How does FOC compare to other approaches, e.g. a sinusoidal drive, with regards to dynamic range?“.

In this article I approach FOC from a somewhat different perspective, which I actually started to like a lot as it shines light on various aspects of FOC in a rather natural way. I of course do not reinvent the wheel, it’s just another view on the problem. The basic idea is to analyze the situation in the $\alpha\beta$ frame and not the rotor-fixed $dq$ frame as it is usually done.

The hobby brushless motors should be classified as Brushless DC Motor (BLDCM), since their back EMF is closer to a trapezoidal shape, and not the sinusoidal shape characteristic for a Permanent Magnet Synchronous Motor (PMSM) (the back EMF of a typical hobby brushless motor has quite strong higher-harmonic contributions). Despite that, in the context of FOC they are treated as PMSMs. This point should be kept in mind, since it can have important practical implications. It is sad that hobby motor manufactures do not offer motors which better approximate PMSMs.

As always, the literature on the web had been my only source of information.

In the previous article Brushless Gimbal Direct Drive: Theory and Experiment, I discussed the sinusoidal motor drive. The present article duplicates some of the material found there, but not all, and I repeatedly refer to that previous article. That is, both articles should be viewed as companions.

1. Motor Equations
1.1. Three-Phase Motor Model
1.2. Space Vector Modulation
2. Field Oriented Control
3. Motor Control Viewed in the $\alpha\beta$ Frame
3.1. Field Oriented Control
3.2. Sinusoidal Modulation
3.3. Simplified FOC
3.4. Comparative Discussion
References

1. Motor Equations

1.1. Three-Phase Motor Model
The following motor equations can be found in any literature source on FOC.

The equations in the $dq$ frame are slightly more general than those I’ve used in the article Brushless Gimbal Direct Drive: Theory and Experiment in that they allow for saliency, i.e., different values for $L_d$ and $L_q$ . However, by the reasons given in [HDP06,AK12], for hobby brushless motors saliency should be small, i.e., we can expect $L_d \approx L_q$ . In addition, we will be more interested in the $\alpha\beta$ frame, in which saliency would imply angle dependent inductances complicating the equations. Therefore, $L_d = L_q = L$ will be assumed.

The electrical angle of the motor’s rotor is denoted by $\epsilon$ . It is related to the mechanical angle $\epsilon_m$ via the number $p$ of motor pole pairs: $\epsilon_m = \epsilon/p$ .

In the rotor-fixed $dq$ frame, the motor equations read:

$\begin{array}{l} \Psi_d = L_d i_d + \Psi_p \\[0.75em] \Psi_q = L_q i_q \end{array}$ Eq. (1.1)

$\begin{array}{l} U_d = R i_d + L_d \dfrac{d}{dt} i_d - \dot{\epsilon} L_q i_q \\[0.75em] U_q = R i_q + L_q \dfrac{d}{dt} i_q + \dot{\epsilon} \left( L_d i_d + \Psi_p \right) \end{array}$ Eq. (1.2)

$M = \dfrac{3}{2} p \left( \Psi_d i_q - \Psi_q i_d \right) = \dfrac{3}{2} p \left[ \Psi_p i_q + \left( L_d - L_q \right) i_d i_q \right]$ Eq. (1.3)

In the $\alpha\beta$ frame the equations for a non-salient motor read:

$\left(\begin{array}{c} \Psi_\alpha\\\Psi_\beta \end{array}\right) = L \left(\begin{array}{c} i_\alpha\\i_\beta \end{array}\right) + \Psi_p \left(\begin{array}{c} \cos\epsilon\\\sin\epsilon \end{array}\right)$ Eq. (1.4)

$\left(\begin{array}{c} U_\alpha\\U_\beta \end{array}\right) = R \left(\begin{array}{c} i_\alpha\\i_\beta \end{array}\right) + L \dfrac{d}{dt} \left(\begin{array}{c} i_\alpha\\i_\beta \end{array}\right) + \dot{\epsilon} \Psi_p \left(\begin{array}{c} -\sin\epsilon\\ \cos\epsilon \end{array}\right)$ Eq. (1.5)

$M = \dfrac{3}{2} p \Psi_p \left( i_\beta \cos\epsilon - i_\alpha\sin\epsilon \right)$ Eq. (1.6)

The back EMF or the term $\Psi_p (\cos\epsilon,\sin\epsilon)$ , respectively, is manifestly sinusoidal, reflecting the PMSM approximation. As in the previous article I find it more convenient to express the $\alpha\beta$ equations using a complex notation, $\hat{x} = x_\alpha + j x_\beta = x_0 e^{j\varphi}$ . This results in

$\hat{\Psi} = L \hat{i} + \Psi_p e^{j\epsilon}$ Eq. (1.7)

$\hat{U} = R \hat{i} + L \dfrac{d}{dt} \hat{i} + j \Psi_p \dot{\epsilon} e^{j\epsilon}$ Eq. (1.8)

$M = \dfrac{3}{2} p \Psi_p \text{Im}[ \hat{i} e^{-j\epsilon}]$ Eq. (1.9)

The motor is driven by applying sinusoidal voltages to the motor phases. Thus also the currents are sinusoidal, and the voltages and currents can be expressed as

$\hat{U} = U_0 e^{j\theta}$ , $\hat{i} = i_0 e^{j\zeta}$ Eq. (1.10)

where $\theta$ and $\zeta$ are the phases and $U_0$ and $i_0$ are the amplitudes of the voltage and current vectors, respectively. This leads directly to

$U_0 e^{j(\theta-\epsilon)} = ( R + j L \dot{\zeta} ) i_0 e^{j(\zeta-\epsilon)} + j \Psi_p \dot{\epsilon}$ Eq. (1.11)

and our „master“ equation:

$M = \dfrac{3}{2} p \Psi_p i_0 \sin(\zeta-\epsilon) = \dfrac{3}{2} p \Psi_p \text{Im}\left[ \dfrac{ U_0 e^{j(\theta-\epsilon)} - j \Psi_p \dot{\epsilon}}{R + j L \dot{\zeta}}\right]$ Eq. (1.12)

Comment: One could, maybe more directly, have also expressed the $dq$ expressions in complex notation, using $\bar{x} = x_d + j x_q = x_0 e^{j\varphi}$ . One would then find the relation $\bar{x} = \hat{x} e^{-j\epsilon}$ , or $\bar{U} = U_0 e^{j(\theta-\epsilon)}$ and $\bar{i} = i_0 e^{j(\zeta-\epsilon)}$ (see also the Formulary here).

1.2. Space Vector Modulation
In practical applications of FOC, the voltages applied to the motor phases are generated from a DC voltage using the PWM technique. The simplest approach would be to directly generate sinusoidal voltages, by using PWM modulation times calculated from $U_0 e^{j(\theta-\epsilon)}$ . However, usually the space vector modulation (SVM) technique is applied. Here, the neutral-point voltage is not zero (or half the bus voltage in fact), but permanently shifted around such that the three generated line voltages „fit better“ into the range given by the DC bus voltage. An excellent explanation is given in [DW14] (starts at ca. 24:00). Other methods such third harmonic injection do also exist.

As a result, for a symmetric motor, the magnitude $U_0$ of the voltages between the motor phases can be larger by about 15% than with using the naive sinusoidal modulation technique. However, also the SVM technique results in sinusoidal phase-to-phase voltages. That is, the description in Chapter 1.1 can be taken over without modification, except that $U_0$ is not limited by (half) the DC bus voltage, but can be larger by a factor 1.15.

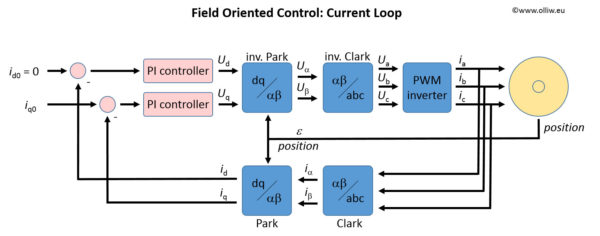
2. Field Oriented Control

Following the standard argument, the FOC algorithm is obtained as follows: In the rotor-fixed frame the voltages and currents are nearly static, slowly time-varying quantities. They are thus much easier to control than the fast time-varying signals in the stator-fixed frame, since a lower controller bandwidth is acceptable. Thus, instead of controlling the phase currents $(i_a, i_b, i_c)$ or the stator-fixed currents $(i_\alpha, i_\beta)$ , the current controller is set up to control the rotor-fixed currents $(i_d, i_q)$ . Since however only $(i_a, i_b, i_c)$ are measurable, and the transformation to the $dq$ frame requires knowledge of the motor position $\epsilon$ , the sensored FOC scheme is immediately obtained:

In normal operating conditions, the direct current $i_d$ is regulated to be zero. The current is then „perpendicular“ to the flux, and the torque generated by the motor is maximal, and given by:

$M = \dfrac{3}{2} p \Psi_p i_q$ Eq. (2.1)

The torque is directly determined by a current, $i_q$ , exactly as it is for a brushed DC motor. As a result, the motor behavior is also that of a brushed DC motor, with a torque constant $k = \frac{3}{2} p \Psi_p$ .

In practice only two of the three phase currents need to be measured, since they are related by $i_a + i_b + i_c = 0$ . Also, the inverse Park transformation can be combined with the SVM into a simpler algorithm. These are however just technical details irrelevant to the principle.

The performance of the current controller can be improved. The $dq$ equations for the voltages are coupled, i.e., the direct voltage $V_d$ is affected not only by $i_d$ but also by $i_q$ , and similarly for the quadrature voltage $V_q$ . Thus, in the above scheme the two PI controllers are coupled, but can be decoupled by adding feedforward terms, which exactly compensate for the coupling terms in the $dq$ equations [AZ05][DL16].

3. Motor Control Viewed in the $\alpha\beta$ Frame

My interest in the FOC technique is related to my efforts in camera gimbals, specifically the 3-axis gimbal controller STorM32. The main question of concern to me was understanding the advantages and disadvantages of the FOC approach in comparison to the simpler sinusoidal modulation technique, as explored in the article Brushless Gimbal Direct Drive: Theory and Experiment, and other FOC-inspired „encoder“ approaches. I found it difficult to find answers with working in the $dq$ frame, as it’s typically done in discussions on FOC. Interestingly, and maybe surprisingly, the $\alpha\beta$ frame, which I found useful for discussing the sinusoidal modulation, turned out to be also useful for discussing FOC.

To simplify notation, the torque constant $k = \frac{3}{2} p \Psi_p$ is introduced.

3.1. Field Oriented Control
The FOC approach as described in the previous Chapter 2 realizes $i_d=0$ . The current is thus perpendicular to the flux orientation (which coincides with the rotor orientation), which implies for the phase $\zeta$ of the current that $\zeta = \pi/2 + \epsilon$ . Thus, equation (1.12) directly leads to

$M = k i_0$ Eq. (3.1)

which of course agrees with the result obtained in Chapter 2.

In the FOC scheme the control variable for controlling the motor is the amplitude of the current $i_0$ .

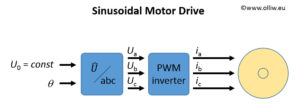
3.2. Sinusoidal Modulation
The case of a sinusoidal modulation has been discussed already in Brushless Gimbal Direct Drive: Theory and Experiment. Here, the motor is driven with the voltages $(U_a,U_b,U_c) = U_0 [\cos\theta,\cos(\theta-\frac{2\pi}{3}),\cos(\theta-\frac{4\pi}{3})]$ .

From equation (1.12) one deduces

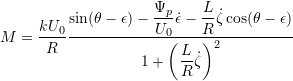$M = \dfrac{k U_0}{R} \dfrac{ \sin(\theta-\epsilon) - \dfrac{\Psi_p}{U_0} \dot{\epsilon} - \dfrac{L}{R}\dot{\zeta} \cos(\theta-\epsilon)}{ 1+ \left( \dfrac{L}{R}\dot{\zeta} \right)^2}$ Eq. (3.3)

With the assumption of low frequencies, $L\dot{\zeta}/R \ll 1$ , and small deviations $\theta-\epsilon \approx 0$ , the simplified torque relation is obtained:

$M = \dfrac{k p U_0}{R} \theta_m - \dfrac{k p U_0}{R} \epsilon_m - \dfrac{k p \Psi_p}{R} \dot{\epsilon_m}$ Eq. (3.4)

where angles were also converted to mechanical angles. Most notably, a term linear in $\epsilon_m$ appears, which will lead to an (undesirable) oscillating characteristic behavior. The term linear in $\dot{\epsilon}$ will add to the damping in the system, and is not very consequential.

The control variable in this drive scheme is the phase $\theta$ of the voltage vector applied to the motor. The amplitude of the voltage $U_0$ is held constant.

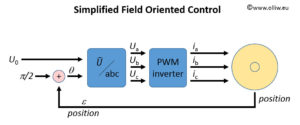
3.3. Simplified FOC
It is interesting to consider a „simplified FOC“ scheme, in which the voltage is maintained to be perpendicular to the flux, and no the current. In other words, instead of enforcing $\zeta = \pi/2 + \epsilon$ one ensures $\theta = \pi/2 + \epsilon$ . This can always be easily achieved with knowing the motor position $\epsilon$ .

From equation (1.12) one then finds

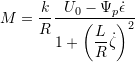$M = \dfrac{k}{R} \dfrac{ U_0 - \Psi_p \dot{\epsilon} }{ 1+ \left( \dfrac{L}{R}\dot{\zeta} \right)^2}$ Eq. (3.5)

Assuming again low frequencies, $L\dot{\zeta}/R \ll 1$ , and converting to mechanical angles, the torque relation simplifies to

$M = \dfrac{k}{R} U_0 - \dfrac{k p \Psi_p}{R} \dot{\epsilon_m}$ Eq. (3.6)

In practical applications the voltage $U_0$ is adjusted by PWM modulation of a DC bus voltage $V_0$ , that is $U_0 = V_0 d$ , with the PWM duty cycle $d$ . The torque relation then reads

$M = \dfrac{k V_0}{R} d- \dfrac{k p \Psi_p}{R} \dot{\epsilon_m}$ Eq. (3.7)

In this method, the control variable is the amplitude $U_0$ of the voltage vector applied to the motor, or the PWM duty cycle $d$ , respectively. The phase $\theta$ is, as mentioned before, adjusted to be always perpendicular to the flux orientation.

3.4. Comparative Discussion
Using the „master equation“ (1.12) three different motor drive schemes could be derived on an equal footing: FOC, a simplified FOC scheme, and the sinusoidal motor drive.

Taking into account the mechanical properties of the motor and a load attached to it, the equation of motion becomes

$J \ddot{\epsilon_m} = M - b \dot{\epsilon_m}$ Eq. (3.8)

where $J$ is the combined moment of inertia of the motor and the load, and $b$ describes some viscous friction. In low-speed operation also a Coulomb friction term of the form $-a|\epsilon_m|$ should be added, but it is more involved to handle mathematically and hence ignored here. Cogging torque would lead to an additional, position dependent term $-M_{cog}(\epsilon_m)$ . Variations in the flux linkage density would by accounted for by an angle dependent friction term $-b_{flux}(\epsilon_m)\dot{\epsilon_m}$ . These contributions to torque ripples [JH96] are in no means negligible in our hobby brushless motors, but are neglected in the following.

We arrive at these transfer functions for the mechanical motor position:

FOC: $\dfrac{\epsilon_m}{i_0} = \dfrac{ k }{ J s^2 + b s}$ Eq. (3.9)

simplified FOC: 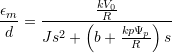$\dfrac{\epsilon_m}{d} = \dfrac{ \frac{k V_0}{R} }{ J s^2 + \left(b + \frac{k p \Psi_p}{R}\right) s}$ Eq. (3.10)

sinusoidal drive: 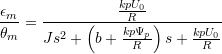$\dfrac{\epsilon_m}{\theta_m} = \dfrac{ \frac{k p U_0}{R} }{ J s^2 + \left(b + \frac{k p \Psi_p}{R}\right) s + \frac{k p U_0}{R} }$ Eq. (3.11)

where in the last two cases the low-frequency $L\dot{\zeta}/R \ll 1$ assumption were employed.

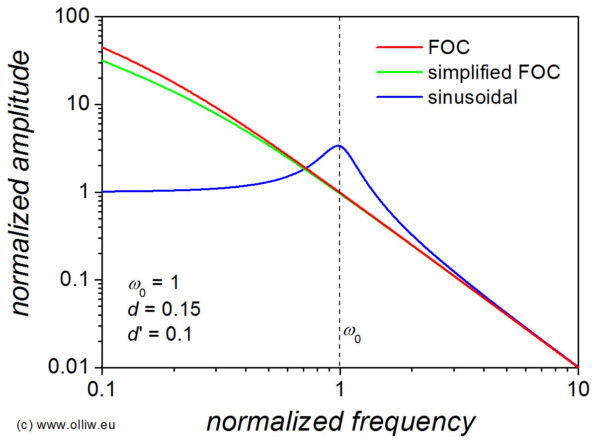
These transfer functions directly reveal the relevant dynamical differences:

In comparison to FOC, the simplified FOC scheme adds a term $kp\Psi_p/R$ to the damping. I unfortunately do not have good values for $k$ (nor for $b$ ), but estimates indicate that this damping is extremely small, and irrelevant. The major difference between the FOC and the simplified FOC schemes is thus that in the latter the effect of the motor inductance kicks in at frequencies of about $L\dot{\zeta}/R \approx 1$ , leading to an additional second-order roll off. Again, I unfortunately do not have good values for $L/R$ ; my estimates range from few 10 Hz to several 10 kHz so that this effect could indeed be significant. In anyway, a general lesson can be learned however:

The major effect of the current control loop is to compensate for the (negative) impact of the motor inductance.

In hindsight I realized that I could have come to that insight already earlier from comparing the dynamics of the voltage- and current-controlled DC motor (discussed here), but I didn’t. This however just underpins the generality of that conclusion.

The major difference of the sinusoidal drive in comparison to the FOC and simplified FOC schemes is the appearance of the term $k p U_0/R$ in the denominator, which has dramatic consequences: The transfer function becomes that of an under-damped oscillator, with a resonance frequency $\omega_0 = \sqrt{k p U_0/RJ}$ (for details see Brushless Gimbal Direct Drive: Theory and Experiment). In practical cases, this frequency is in the range of 5 – 15 Hz, which implies that the motor loses its responsiveness at frequencies above this cut off.

Frequency Dependencies
The similarities and differences in the dynamic behavior can be further underpinned by rewriting the transfer functions as follows:

FOC: $H(s) \propto \dfrac{ 1 }{ s^2 + 2 d' \omega_0 s}$ Eq. (3.12)

simplified FOC: $H(s) \propto \dfrac{ 1 }{ s^2 + 2 d \omega_0 s}$ Eq. (3.13)

sinusoidal drive: $H(s) \propto \dfrac{ 1 }{ s^2 + 2 d \omega_0 s + \omega_0^2}$ Eq. (3.14)

where $d' \le d$ , $2 d \omega_0 = b/J + k p \Psi_p / RJ$ , and $\omega_0$ as before. For the simplified FOC and sinusoidal drive schemes the roll-off due to the motor inductance at frequencies above $L\dot{\zeta}/R \approx 1$ have in addition to be rated in.

Parameter Identification
For the simplified FOC scheme, the transfer function with respect to speed can be written as

$\dfrac{ \dot{\epsilon}_m }{ U_0 } = \dfrac{ K }{ 1 + Ts }$ Eq. (3.15)

with parameters

$K = \dfrac{ k }{R J} \, \dfrac{ J }{b + \frac{k p \Psi_p}{R} } = \dfrac{ 1 }{ \frac{b}{k} R + p \Psi_p }$ $T = \dfrac{ J }{ b + \frac{k p \Psi_p}{R} } = \dfrac{ R J}{ k } K$ Eq. (3.16)

Notably, $K$ is independent of the inertia $J$ and thus is indeed a motor constant. In the steady state or constant speed operation one finds

$\dot{\epsilon}_m = K U_0$ Eq. (3.17)

The constant $K$ can be compared to the motor constant $1/k_0$ or $1/k'$ , respectively, of the DC motor (eqs. 3.1 and 3.2 in Elektromotor & Rotor: Grundlagen), yielding $k_U = p \Psi_p$ and $k_M = k = \frac{3}{2} p \Psi_p$ . That is, the motor equation Eq. (3.6) for the simplified FOC scheme can also be written as