Digital Filters

I present some basic material on digital filters, along with interactive plots to visualize their properties and help in filter design. The compilation is essentially my reference book, but maybe you’ll find it useful too.

1. Basics
  1.1. Basic Relations
  1.2. Biquads
2. First-order Low Pass Filter
  2.1. Continuous Time
  2.2. Backward Difference, LPF1  (with interactive plot)
  2.3. Bilinear, LPF2  (with interactive plot)
3. CIC Filter, Average  (with interactive plot)
4. Second-order Low Pass Filter
  4.1. Continuous Time  (with interactive plot)
  4.2. Backward Difference, LPF3
  4.3. Bilinear, LPF4  (with interactive plot)
  4.4. Cascaded First-order Low Pass Filters, LPF5
  4.5. Butterworth, LPF6
  4.6. Biquad
5. Second-order Inverse Chebyshev Low Pass Filter
  5.1. Continuous Time
  5.2. Biquad, LPF7  (with interactive plot)
6. Second-order Peaking and Notch Filter
  6.1. Continuous Time
  6.2. Biquad
7. Design Tools
  7.1. CIC + Biquad Low Pass Filter
  7.2. CIC + Inverse Chebyshev Biquad Low Pass Filter
Appendix

1. Basics [1|2|3|4|5|6|7|A]

1.1. Basic Relations
For a continuous-time transfer function the frequency response is calculated by substituting , where is the real frequency. The frequency response of a discrete-time transfer function is calculated by substituting

  ,

where is the real frequency, and the sampling time step. The sampling rate is

  .

Whenever the domain is obvious from the context, the super- and/or subscripts to the transfer function are dropped, and , and written for simplicity.

The response of the discrete-time transfer function at zero frequency is given by , and that at the Nyquist frequency by .

In order to derive from a continuous-time transfer function , usually the variable is substituted by different approximations. Typical choices are:

backward difference:	,	Eq. (1.2)
bilinear transformation, expansion of :	,	Eq. (1.3)

These approximations represent non-linear mappings from continuous-time to discrete-time. For the bilinear transform, the effect is completely captured by warping the frequency axis according to

  ,

where and are the continuous-time and discrete-time frequencies, respectively.

The phase delay is defined as

  .

Its meaning is clarified by the relation . For a linear-phase filter holds , corresponding to a constant phase delay of .

The group delay is defined as

  .

1.2. Biquads
A common implementation of second-order filters uses a biquad. The transfer function is

  ,

and the difference equation reads

  .

The biquad is quite general and can produce many different filters. For a low-pass filter, with unit zero-frequency gain or , the coefficients are restricted to .

Often the bilinear transform is used to generate the biquad coefficients from a continuous-time transfer function . The continuous-time frequency is typically normalized to some characteristic time , or characteristic frequency , i.e., is written in terms of the variable . One finds:

  ,

  .

The coefficients in should be normalized by to yield the biquad form used in this article. The value of may be corrected with the warping formula, to match the response of the discrete-time filter with the response of the continuous-time filter at e.g. the characteristic frequency: .

The code for implementing biquads is quite straight forward.

  datatype y, num;
  num = a0 * x + a1 * regX1 + a2 * regX2;
  y = num - b1 * regY1 - b2 * regY2;
  regX2 = regX1;
  regX1 = x;
  regY2 = regY1;
  regY1 = y;
  return y; //the return value usually will have fewer bits than datatype


  datatype y;
  reg0 = x - b1 * reg1 - b2 * reg2;
  y = a0 * reg0 + a1 * reg1 + a2 * reg2;
  reg2 = reg1;
  reg1 = reg0;
  return y;


  datatype y;
  y = a0 * x + reg1;
  reg1 = a1 * x - b1 * y + reg2;
  reg2 = a2 * x - b2 * y;
  return y;


In some cases the coefficients can be represented by integers resulting in more efficient fixed point code. This is filter dependent, and thus discussed in the corresponding chapters.

• Biquads by Nigel Redmon
• Biquad calculator v2 by Nigel Redmon
• Pole-Zero placement v2 by Nigel Redmon
• Filter frequency response grapher by Nigel Redmon
• Iowa Hills Software, IIR Filter Design
• Iowa Hills Software, IIR Filter Design Using the Bilinear Transform
• Designing and implementing biquad IIR filters with the ASN Filter Designer: a tutorial review by Advanced Solutions Netherlands

2. First-order Low Pass Filter [1|2|3|4|5|6|7|A]

2.1. First-order Continuous Time
The continuous-time transfer function of a first-order low-pass filter (LPF) reads:

  .

The amplitude is

  ,

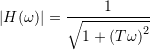and the cut-off frequency is

  .

By using either the backward difference or the bilinear transformation for substituting , two different discrete-time LPFs are derived.

2.2. First-order Backward Difference, LPF1
With a suitable parameterization, the discrete-time transfer function is obtained as

  ,

  .

The difference equation becomes

  ,

which is probably the most frequently used version of a first-order LPF.

The amplitude frequency dependence is given by

  .

It exhibits neither a zero nor a pole in the entire frequency range. The cutoff frequency of the corresponding continuous-time filter is

  .

However, the frequency axis is warped, and the -3 dB cutoff frequency of the discrete-time filter is shifted to lower values, according to

  .

The filter constant maybe chosen such that it is represented exactly in integer arithmetic, that is

 

where is an integer with . The filter is then represented by the equations

  ,

  .

The following settings can be realized:

Hz	ms	Hz	Hz

   log   phase
First-order Backward Difference LPF: Discrete-time first-order LPF derived from backward difference, for integer inverse filter constant.

2.3. First-order Bilinear, LPF2
With a parameterization ensuring and , the discrete-time transfer function is obtained as

  ,

  .

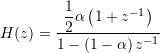The difference equation becomes

  .

The amplitude frequency dependence is given by

  .

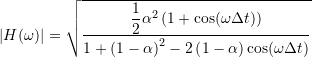It exhibits a zero at or the Nyquist frequency . It has no poles in the entire frequency range. The cutoff frequency of the corresponding continuous-time filter is

  .

However, the frequency axis is warped, and the -3 dB cutoff frequency of the discrete-time filter is shifted to lower values, according to

  .

Note: This can be derived directly from the above equations, or from using the bilinear transform warping formula given in Chapter 1.1.

It is often convenient to chose the filter constant such that it is represented exactly in integer arithmetic. Two options emerge depending on how the factor is handled. For instance:

  ,

where is an integer with . The filter is then represented by the equations

  ,

  .

The following settings can be realized:

Hz	ms	Hz	Hz

   log   phase
First-order Bilinear LPF: Discrete-time first-order LPF derived from bilinear transformation, for integer inverse filter constant.

3. CIC Filter, Average [1|2|3|4|5|6|7|A]

Up to a normalization constant, the (one-stage) CIC and moving average filters are equivalent. They are FIR filters with a low-pass characteristic, and have no continuous-time counterpart.

The discrete-time transfer function of a moving average reads:

  ,

where is the number of samples averaged. The difference equation reads

  ,

where the last expression points to the recursive calculation of the moving average.

The amplitude frequency dependence is

  .

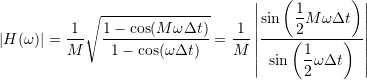It exhibits zeros at or , with integer and . It has no poles. The frequency of the first zero is

  ,

and represents the passband edge. The moving average filter has quite significant attenuation in the passband, and the -3 dB frequency lies below half of the frequency of the first zero:

      for ,
    for .

The impulse response of the moving average is symmetric, and the filter is therefore a linear-phase filter, with a delay of samples or . The phase at the -3 dB frequency is thus roughly , and at the first zero equal to .

• Understanding cascaded integrator-comb filters by Richard Lyons.
• Useful results on the stopband behavior and approximation by a first-order LPF, link.

Hz	Hz	Hz

   log   phase
CIC Filter: Discrete-time moving average filter, for averaging length .

4. Second-order Low Pass Filter [1|2|3|4|5|6|7|A]

4.1. Second-order Continuous Time
The continuous-time transfer function of a second-order low-pass filter can be written as

  ,

but many alternative parameterizations are in use. The characteristic frequency is

  ,

and is the damping parameter, where corresponds to an over-damped and to an under-damped system. Accordingly, for the transfer function exhibits two real poles, and for a complex conjugated pair of poles. The quality factor is given by .

The amplitude and phase are

  ,    ,

and the cut-off frequency is

  .

For , the amplitude exceeds unity in the pass band, with a maximum at

     ,

and passes again through unity gain at the frequency

  .

		–	–	–
		–	–	–
			dB
Hz	Hz	Hz		Hz

   log   phase
Continuous Time Second-order LPF: Continuous-time second-order LPF, for specified damping , in relation to the characteristic frequency .

4.2. Second-order Backward Difference, LPF3
The discrete-time transfer function assumes the following structure

  ,

with two parameters and , which are related to and as

  ,    ,

The difference equation becomes

  .

4.3. Second-order Bilinear, LPF4
With a paramterization ensuring and , the discrete-time transfer function assumes the following structure

  ,

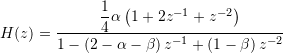with two parameters and , which are related to and as

  ,     ,     ,

or then inverted

  ,    .

The difference equation becomes

  .

The amplitude frequency dependence exhibits a zero at or the Nyquist frequency . The frequency axis is warped, and the -3 dB cutoff frequency of the discrete-time filter is shifted to lower values, according to

  ,

where is the cutoff frequency of the continuous time filter given in Chapter 4.1. Analogous relations hold for the the frequencies of the maximum and the unity gain crossing, and . The height of the maximum is not affected by the warping, and is identical to .

Hz	ms	Hz	Hz	Hz
= Hz    = dB    = Hz

   log   phase
Second-order Bilinear LPF: Discrete-time second-order LPF derived from bilinear transformation.

4.4. Cascaded First-order Low Pass Filters, LPF5
For , the second-order LPF reduces to a cascade of two identical first-order LPFs, each with time constant .

Only the bilinear filter is considered. The constants and reduce to and , where is the -constant of the first-order LPF (LPF2), and the discrete-time transfer function becomes

  .

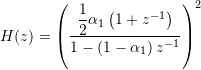This leads to a straight forward and cheap implementation. The frequency response is however not very desirable. The crossover region is „smeared“ out, and the cutoff frequency (of the continuous-time transfer function) is shifted down to , see also the table given in Chapter 4.1.

4.5. Second-order Butterworth, LPF6
For , the most flat passband together with narrowest transition range is achieved. The continuous-time cutoff frequency matches the characteristic frequency, . Commonly the filter is implemented using a biquad.

One may chose the filter constant such that it is represented exactly in integer arithmetic. For instance:

 

where is an integer with . The filter is then represented by the equations

  ,

  .

The multiplication with can be executed approximately but efficiently by choosing two integers and , such that , and thus

  .

An interesting approximation is given by

which corresponds to the difference equations

  ,

  .

4.6. Biquad
For biquads see Chapter 1.2. For a low-pass filter, with unit zero-frequency gain and a zero at the Nyquist frequency, the biquad coefficients have to fulfill

  ,
  ,

yielding the parameterization in Chapter 4.3.

5. Second-order Inverse Chebyshev Low Pass Filter [1|2|3|4|5|6|7|A]

The inverse Chebyshev, or Chebyshev Type II, low-pass filter has some nice features. Especially, it provides a sharp transition region, which makes it e.g. a nice anti-aliasing filter, and at the same time retains a good phase behavior, comparable to a Butterworth filter. However, for even-order filters the passband attenuation stays finite at high frequencies, and odd-order filters are preferred from that perspective. In addition, for the discrete-time filter I could not find a single setting of interest which could be realized with integer-valued parameters, i.e., one needs to resort to a full biquad implementation, and pay attention to its pain-points when using fixed-point arithmetic.

5.1. Inverse Chebyshev Continuous Time
The amplitude frequency response of a second-order inverse Chebyshev low-pass filter is given by

  ,

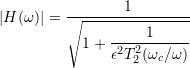with the Chebyshev polynomial , the characteristic frequency , and the ripple parameter .

The -3 dB cut-off frequency , the frequency location of zero amplitude , and the gain in the stopband are given by

  ,    ,    .

The characteristic frequency is generally considered as passband edge, and corresponds to the frequency where the amplitude falls below the stopband gain factor the first time.

The transfer function is

  ,

with the zeros and poles located at

  ,    ,

• Chebyshev Filters by John Stensby.
• Chapter 5: Chebyshev Type II Filters, author unknown.
• Linear Digital Filtering I: Part IV Design of IIR filters, author unknown.

5.2. Inverse Chebyshev Biquad, LPF7
The math involved with Chebyshev filters is somewhat lengthy. However, it can be bypassed by applying this set of conditions in the determination of the biquad coefficients:

• (i) location of the zero-gain frequency 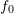, implying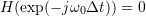
• (ii) gain 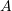in the stopband, implying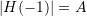
• (iii) unity gain at zero frequency, implying
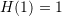
• (iv) zeros are conjugated complex pairs on the unit circle
• (v) poles are conjugated complex pairs within the unit circle

The filter coefficients are then uniquely determined by three parameters, the frequency of the zero , the gain in the stopband , and a third parameter which governs the behavior in the passband. The value of this third parameter would be fixed by requiring a Chebyshev characteristic. However, it is useful to keep it as a tuning parameter, which implies that the filter below is not strictly an inverse Chebyshev filter, but more general.

The discrete-time transfer function can be expressed as

  ,

with zeros at and , and poles at and , where . The frequency response is then

  .

The free parameters are chosen as the zero-gain frequency , the stopband gain , and the magnitude of the pole . The remaining values are then given by

  ,

  ,

  .

Inverse Chebyshev characteristic would be achieved by choosing according to

  .

dB
Hz	Hz
= Hz    = Hz    = dB    = Hz

   log   phase
Inverse Chebyshev LPF: Discrete-time second-order inverse Chebyshev LPF based on a biquad with a generalized paramterization. Comment: The characteristic values are determined numerically.

6. Second-order Notch and Peaking Filter [1|2|3|4|5|6|7|A]

The notch filter is ideal for filtering out one specific frequency. While the notch filter has a zero at the center frequency , a variant of it often refereed to as peaking filter allows us to set the gain (attenuation) at . The notch filter is then recovered for infinite attenuation. The peaking filter is thus more versatile and considered here, but also often refered to as notch filter.

6.1. Continuous Time
The frequency response of a second-order peaking filter is given by

 

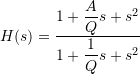
The notch filter corresponds to . The following, equivalent formulations are also often found:

  ,   

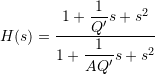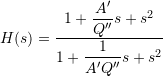
Note: The peak filter can be derived from a band-pass filter in several ways, e.g.: or or , corresponding to the three given forms. The meaning of changes thereby.

This gives rise to a multitude of equations which can be found on the web. In this article the first version is prefered, since here has the „usual“ meaning as it is known for the second-order low-pass, band-pass, and high-pass filters.

The definition of „bandwidth“ becomes somewhat fuzzy and allows for several possibilities, which further increases the number of equations found on the web. It is especially reminded that for the band-pass filter , which underlies the peaking filter, it strictly holds

 

whereas

 

holds only approximately, for large values of . Here, and are the lower and upper -3 dB frequencies, and the bandwidth would be defined as . For a peaking filter with gain this also would be an appropriate definition of bandwidth. However, for a peaking filter with attenuation the frequencies and do in general not correspond to the -3 dB points.

6.2. Biquad
The biquad coefficients can be derived by applying this set of conditions:

• (i) unity gain at zero frequency, implying
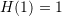
• (ii) unity gain at the Nyquist frequency, implying
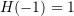
• (iii) location of the center frequency 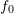and pass-through amplitude 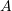, implying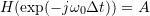
• (iv) bandwidth 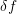at the center frequency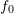

The filter coefficients are then uniquely determined by three parameters, the center frequency , the pass-through amplitude at the center frequency, and a third parameter which relates to the bandwidth.

The discrete-time transfer function can be expressed in many equivalent ways, which differ in how the biquad coefficients are parameterized. In fact, quite many different parameterizations can be found on the web, too many to be all discussed here. Most of these equations are obtained from discretizing the continous-time transfer function using the bilinear transformation.

A simple parameterization, which follows quite directly from imposing the above set of conditions, is

  .

Here, the attenuation at the center frequency is directly specified by . The parameter is related to the bandwidth (in a non-linear fashion). The equation is sometimes also written in the more „normalized“ fashion

 

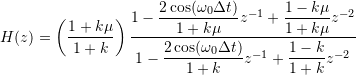
with obvious relations between the , and , parameters.

Another frequently found set of equations is obtained by pre-warping the bilinear transformation, i.e., by using , where . This results in

 

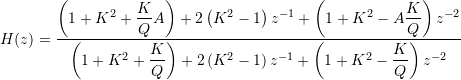
with obvious relations of its parameters to the above , parameters. It should be noted however that the applied warping only matches the center-frequency of the discrete-time filter to that of the continuous-time filter, but not e.g. and . Therefore, the frequency response of the discrete-time filter will in general be distorted, and its actual bandwidth be different from that of the continuous-time filter. In short, the „bandwidth“ used in this sort of equations is not a precisely defined aspect of the discrete-time filter’s frequency response but more of a figure-of-merit, which more or less represents the actual bandwidth.

Note: ,

* http://www.eng.ucy.ac.cy/cpitris/courses/ECE623/presentations/DSP-LECT-20.pdf
* https://github.com/libaudioverse/libaudioverse/blob/master/audio%20eq%20cookbook.txt
* http://shepazu.github.io/Audio-EQ-Cookbook/audio-eq-cookbook.html
* https://pdfs.semanticscholar.org/56e6/1c03d338c293afa6cbb470b11d360195cf5f.pdf
* https://www.dummies.com/education/science/science-engineering/how-to-characterize-the-peaking-filter-for-an-audio-graphic-equalizer/
* https://ccrma.stanford.edu/~jos/fp/Peaking_Equalizers.html
* https://www.dsprelated.com/freebooks/filters/Peaking_Equalizers.html
* http://www.advsolned.com/allpass-peaking-bell-filter/
* bilinear pre-warped z transform: https://www.earlevel.com/main/2003/03/02/the-bilinear-z-transform/
* bandwidth in octaves: https://www.rane.com/note170.html
* http://dspguide.com/ch19/3.htm

7. Design Tools [1|2|3|4|5|6|7|A]

The combination of a one-stage CIC filter with a biquad can yield efficient and/or effective anti-aliasing filters, useful for instance for downsampling in real-time applications.

• Multirate DSP, part 1: Upsampling and downsampling by Li Tan
• Polynomial Interpolators for High-Quality Resampling of Oversampled Audio by Olli Niemitalo

7.1. CIC + Biquad Low Pass Filter

LPF order			CIC order
none1. order backward1. order bilinear2. order			none1 stage
Hz	ms
= Hz    = Hz    = dB    = Hz
= = 1/    = = 1/

   log   phase
CIC + Biquad LPF: Discrete-time moving average plus first- or second-order LPF derived from bilinear transformation. Comment: The characteristic values are determined numerically.

Example settings:

12	3.20156	0.46852	1/12	1/4	0.04372
12	2.63629	0.30346	1/8	1/5	0.05581
3	0.59161	0.33806	5/4	1/2	0.02183

7.2. CIC + Inverse Chebyshev Biquad Low Pass Filter

			CIC order
dB			none1 stage
Hz	Hz
= Hz    = Hz    = dB    = Hz
= = 1/    = = 1/ =   = = 1/    = = 1/

   log   phase
CIC + Inverse Chebyshev LPF: Discrete-time moving average plus second-order inverse Chebyshev LPF based on a biquad usinga generalized parameterization. Comment: The characteristic values are determined numerically.

Appendix [1|2|3|4|5|6|7|A]

A.1. References

• http://www.micromodeler.com/dsp/
• Iowa Hills Software, Digital and Analog Filters
• Iowa Hills Software, IIR Filter Design
• Iowa Hills Software, IIR Filter Design Using the Bilinear Transform
• Matheonics Tutorial
• Understanding cascaded integrator-comb filters by Richard Lyons
• Useful results on the stopband behavior and approximation by a first-order LPF, link
• Biquads by Nigel Redmon
• Biquad calculator v2 by Nigel Redmon
• Pole-Zero placement v2 by Nigel Redmon
• Filter frequency response grapher by Nigel Redmon
• Designing and implementing biquad IIR filters with the ASN Filter Designer: a tutorial review by Advanced Solutions Netherlands
• Chebyshev Filters by John Stensby
• Chapter 5: Chebyshev Type II Filters, author unknown
• Linear Digital Filtering I: Part IV Design of IIR filters, author unknown
• Multirate DSP, part 1: Upsampling and downsampling by Li Tan
• Polynomial Interpolators for High-Quality Resampling of Oversampled Audio by Olli Niemitalo

 
A.2. Poles and Zeros

The continuous-time transfer function may be written in terms of its poles and zeros as

  ,

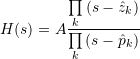with a constant , and the (complex valued) zeros and poles , written as

  ,    .

The squared magnitude of the frequency-dependent transfer function then becomes

  ,

which has complex conjugated pairs of zeros at

  ,    ,

and complex conjugated pairs of poles at

  ,    .

From determining the zeros and poles of one thus can straightforwardly conclude the zeros and poles of , selecting the poles in the left-half plane, , for the stability of .

Example: Second-order LPF
We consider a second-order LPF, with written as

  .

Now shall be assumed. The poles are then determined to

  ,

  ,

  ,

  ,

where in the last step the complex square roots were evaluated. This yields the poles

  ,

with phases chosen such that the poles are in the left-half plane. One finally obtains

  .

 
A.3. Square Root of a Complex Number

  .

 
A.4. Bilinear Transformation

  ,   .

With one finds for :

  .

  .

  ,    .

Poles and zeros transform as expected:

  ,

  .

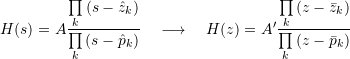Example: Second-order Inverse Chebyshev LPF
Using the method of Chapter A.2., the zero and poles of are determined as

  ,    .

Using the notation of chapter 5.2, one finds the zeros of as

  ,    .

Considering that and that on the frequency axis , one just has recovered the warping formula applied to . For the poles one finds

  ,    ,    with .

Substituting and exploiting the relation yields the result given in Chapter 5.2.

 
A.5. Frequency Response of a Biquad

The frequency response of a biquad

 

is calculated as