The UC4H Airspeed node is a member of the family of UAVCAN nodes I’m working on as part of my UAVCAN for Hobbyists project. The matter of measuring airspeed is relatively complex, and I thus devote an extra page to this sensor, and also cover some fundamentals.
Recently, quite a number of new suitable differential pressure sensors have become available, also using different measurement principles. They all promise to outperform the MS4525DO sensor, which appears to be the established standard in our hobby. A primary motivation of the UC4H Airspeed node is thus to make use of a modern sensor, and ideally the best available. Obviously, I can’t explore them all, and new sensors kind of crop up every day. However, two sensors attracted my interest in particular, and I should acknowledge that I really wasn’t the only one or even the first one who recognized them, namely the RSC TruStability pressure sensors from Honeywell and the DLHR differential pressure sensors from AllSensors.
The UC4H Airspeed node is developed in cooperation with Evan, who especially contributes the practical in-flight testing. Thanks so much, Evan!
1. Differential Pressure Sensors
2. Airspeed Fundamentals
3. International Standard Atmosphere
4. UC4H Airspeed Node
Differential Pressure Sensors
Support of the following digital differential pressure sensors can currently be found in ArduPilot:
-
MS4525DO: typical pressure range ±1 psi = ±6890 Pa
datasheet -
MS5525DSO: typical pressure range ±1 psi = ±6890 Pa
datasheet, discussion thread -
DLVR-L05D: pressure range ±5 inH2O = ±1250 Pa
datasheet -
SDP33: pressure range ±1500 Pa
datasheet, discussion thread, discussion thread
The MS5525DSO has attracted much interest and raised high hopes. However, from the reports so far the experience appears to be mixed. In any case, it exhibits a large dependence on the orientation of the sensor (upwards vs downwards facing), i.e., dependence on acceleration, which was shown to be as large as 8 Pa (see the discussion thread), and also offset. Due to these points, I excluded it from consideration.
The SDP33, offered by Drotek together with a pitot-static tube in a combined package, also was introduced with much hype. It is distinguished by the fact that it actually measures thermal heat flow, and not directly the pressure difference using a membrane as the other sensors. The thermal heat flow depends on the gas flow, which in turn is related to a pressure difference due to the viscosity of air. The different measurement principle has implications. One is a supposedly very accurate and stable zero offset, which allows comparatively accurate measurement at low airspeeds. In the data sheet a zero point accuracy and stability of 0.2 Pa and 0.1 Pa, respectively, are given. However, the span accuracy is comparatively bad, up to ±500 Pa it is only 3 % and at full span only 6 %. Moreover, since it measures flow and not in static conditions, the measurement result depends significantly on the tubing and details of the pitot-static tube, where ’significant‘ means 10 % and larger. This in fact required an explicit calibration of the Drotek sensor, where the corrections amount to a staggering 19 %. It also means that any modification, such as changing the length of the tubes or changing to a different pitot-static tube, makes the calibration useless. In my opinion this limitation is a killer factor, and makes this sensor totally useless for our purposes.
The RSC TruStability pressure sensors look very promising. From the data sheet one can expect a very small dependence on acceleration and orientation, and all accuracy and stability figures are in the low sub-percentage range, e.g., the total error band and accuracy are specified as ±0.25 %FSS and ±0.1 %FSS, respectively.
Also the DLHR sensors, the higher-end family of the DLVR sensors, look very interesting, with similar specs as the RSC sensors. There is an interesting article which compares them to the RSC sensors: https://xdevs.com/article/pressure (thx Evan for point me to it). It is however not clear if for the RSC sensors the auto zero procedure was applied, from the sources in the github repository it doesn’t seem so. This might explain the higher deviations.
A main drawback, at least currently, is that the selection of DLHR and RSC sensors which is available at distributors such as Mouser is still very small. So, sourcing is a bit of an issue.
Presently, it is far from clear which of the newer sensors is the ‚best‘. It will be interesting to see how the DLHR and RSC sensors compare to the other ones, and how they compare to each other, which is another goal of the UC4H Airspeed node project.
Airspeed Fundamentals
Determining the airspeed is relatively complex, since various effects such as the compressibility of air, sensor inaccuracies and inaccuracies due to mounting location of the sensor, and especially the dependency on the atmospheric condition need to be taken into account. Which definition of airspeed is appropriate also depends on the question asked. For instance, the airspeed relevant for judging the aircraft’s flight conditions, which is governed by aerodynamic forces, is not the same as that relevant for navigation. Thus, various airspeeds are introduced, but their relationship is, in principle, simple.
The basic problem in dealing with airspeed can be understood from the equation for the dynamic pressure ![]() , as it appears in the Bernoulli equation:
, as it appears in the Bernoulli equation:
![]() Eq. (1)
Eq. (1)
where ![]() is the velocity of the air flow, or the true airspeed (TAS) in fact, and
is the velocity of the air flow, or the true airspeed (TAS) in fact, and ![]() is the mass density of air. It is to be noted that, first, the Bernoulli equation holds only for ideal fluids, which are incompressible and inviscid. Second, in order to determine
is the mass density of air. It is to be noted that, first, the Bernoulli equation holds only for ideal fluids, which are incompressible and inviscid. Second, in order to determine ![]() from
from ![]() , one obviously needs to know
, one obviously needs to know ![]() , which however cannot be measured directly and must be estimated somehow. It is this latter point, which brings in the complexity.
, which however cannot be measured directly and must be estimated somehow. It is this latter point, which brings in the complexity.
The effect of the air compressibility has been worked out, yielding
![]() Eq. (2)
Eq. (2)
where ![]() is the static pressure and
is the static pressure and ![]() the heat capacity ratio.
the heat capacity ratio. ![]() is the difference between total pressure
is the difference between total pressure ![]() and static pressure,
and static pressure, ![]() , which is sometimes called the ‚ram‘ or ‚impact‘ pressure, and is the pressure measured by a differential pressure sensor connected to a pitot-static tube. At low speeds
, which is sometimes called the ‚ram‘ or ‚impact‘ pressure, and is the pressure measured by a differential pressure sensor connected to a pitot-static tube. At low speeds ![]() , the behavior of the incompressible fluid is retrieved, i.e., the air compressibility becomes relevant only at high speeds. For small, slow-flying aircraft, such as our fixed wing drones, it is generally said that the effects of compressibility is negligible. Indeed, at an airspeed of 50 m/s the correction is only 1 % (for
, the behavior of the incompressible fluid is retrieved, i.e., the air compressibility becomes relevant only at high speeds. For small, slow-flying aircraft, such as our fixed wing drones, it is generally said that the effects of compressibility is negligible. Indeed, at an airspeed of 50 m/s the correction is only 1 % (for ![]() = 1 bar).
= 1 bar).
Determining the air density ![]() is more complicated, and the concepts of a standard atmosphere and of standard sea-level (SSL) parameters as reference points enter here. The aim is to use measurements of the air temperature
is more complicated, and the concepts of a standard atmosphere and of standard sea-level (SSL) parameters as reference points enter here. The aim is to use measurements of the air temperature ![]() and the static pressure
and the static pressure ![]() to estimate
to estimate ![]() . The discussion of this procedure is deferred to the next chapter. We here just accept that reference values
. The discussion of this procedure is deferred to the next chapter. We here just accept that reference values ![]() ,
, ![]() and
and ![]() exist, and refer to them as SSL conditions.
exist, and refer to them as SSL conditions.
True Airspeed, TAS:
This is the velocity of air flow ![]() , and related to the impact pressure and static pressure as given in Eq. (2). Inversion of that equation yields
, and related to the impact pressure and static pressure as given in Eq. (2). Inversion of that equation yields
![]() with
with ![Rendered by QuickLaTeX.com f = \sqrt{ \dfrac{\kappa}{\kappa-1} \dfrac{p_s}{q_c} \left[ \left( \dfrac{q_c}{p_s} +1\right)^{\frac{\kappa-1}{\kappa}} -1\right]} \approx 1 - \dfrac{1}{4\kappa} \dfrac{q_c}{p_s}](https://www.olliw.eu/wp-content/ql-cache/quicklatex.com-c490b837027387fad053b24c7bed123b_l3.png) Eqs. (3), (4)
Eqs. (3), (4)
where ![]() is the the compressibility factor. As before, at low airspeeds or small impact pressures the behavior of an incompressible fluid is recovered.
is the the compressibility factor. As before, at low airspeeds or small impact pressures the behavior of an incompressible fluid is recovered.
Equivalent Airspeed, EAS:
The equivalent airspeed ![]() is, by definition, related to the TAS as
is, by definition, related to the TAS as
![]() Eq. (5)
Eq. (5)
Calibrated Airspeed, CAS:
The calibrated airspeed ![]() is obtained by calibrating the airspeed sensor such that it exactly yields the TAS at standard sea-level conditions. That is, for an aircraft flying at SSL conditions the measured impact pressure yields
is obtained by calibrating the airspeed sensor such that it exactly yields the TAS at standard sea-level conditions. That is, for an aircraft flying at SSL conditions the measured impact pressure yields
![]() with
with ![Rendered by QuickLaTeX.com f_0 = \sqrt{ \dfrac{\kappa}{\kappa-1} \dfrac{p_0}{q_c} \left[ \left( \dfrac{q_c}{p_0} +1\right)^{\frac{\kappa-1}{\kappa}} -1\right]}](https://www.olliw.eu/wp-content/ql-cache/quicklatex.com-0907b716d2868275200d56988c443ea2_l3.png) Eqs. (6), (7)
Eqs. (6), (7)
for all airspeeds (note, the static pressure is fixed to ![]() by the SSL conditions). For an aircraft at non-SSL conditions, the CAS is when defined as
by the SSL conditions). For an aircraft at non-SSL conditions, the CAS is when defined as
![]() Eq. (8)
Eq. (8)
Note that it is implicitly assumed here that the heat capacity ratio ![]() does not depend on the atmospheric conditions. For instance, humid air would need additional corrections.
does not depend on the atmospheric conditions. For instance, humid air would need additional corrections.
Indicated Airspeed, IAS:
The IAS is generally said to be the airspeed indicated by the airspeed measurement device, which then needs to be corrected for sensor imperfections and mounting effects to yield the CAS. The IAS might have been of relevance historically or still is in professional avionics. We however understand that any measurement unit has it’s inaccuracies which need to be accounted for in order to yield reliable data points. The IAS is thus irrelevant to us, and we only consider the CAS.
Relation between CAS, EAS, and TAS:
The relation between EAS and TAS is given by Eq. (5). The relation between CAS and EAS can be established by combining Eqs. (3), (5), and (8), and similar holds for the relation between CAS and TAS. For convenience we summarize all three here:
![]() ,
, ![]() ,
, ![]() Eqs. (9a), (9b), (9c)
Eqs. (9a), (9b), (9c)
As before, for low airspeeds or impact pressures the compressibility factors become close to one, and EAS and CAS are identical in this situation. In fact, the compressibility ratio ![]() deviates from one very slowly with increasing impact pressure, such that the compressibility can be safely neglected in all situations our aircraft usually experiences. It then remains to determine the ratio
deviates from one very slowly with increasing impact pressure, such that the compressibility can be safely neglected in all situations our aircraft usually experiences. It then remains to determine the ratio ![]() to convert from EAS to TAS.
to convert from EAS to TAS.
References I liked:
- Report No. 837: Standard Nomenclature for Airspeeds with Tables and Charts for Use in Calculation of Airspeed, by W. S. AIKEN
- Fluggeschwindigkeiten, IAS, TAS, EAS, CAS, Mach, by wabis
- Report 1364: Measurement of Static Pressure on Aircraft, by W. Gracby
International Standard Atmosphere
As discussed in the previous chapter, in order to convert EAS to TAS, one needs to know the air density ![]() , see Eq. (9a). The problems encountered here are very similar to those encountered in determining the altitude
, see Eq. (9a). The problems encountered here are very similar to those encountered in determining the altitude ![]() from barometric measurements. The procedure consists of measuring the ambient temperature
from barometric measurements. The procedure consists of measuring the ambient temperature ![]() and ambient static pressure
and ambient static pressure ![]() , and to use a model of the atmosphere to determine unknowns such as the air density
, and to use a model of the atmosphere to determine unknowns such as the air density ![]() or the altitude
or the altitude ![]() . The model of the atmosphere obviously will be quite oversimplified and won’t consider effects due to hot or cold days, dry or wet air, clouds, winds, rain, highs and lows, and so on. The task can thus not be strictly achieved.
. The model of the atmosphere obviously will be quite oversimplified and won’t consider effects due to hot or cold days, dry or wet air, clouds, winds, rain, highs and lows, and so on. The task can thus not be strictly achieved.
The model atmosphere, which is mostly used, is the International Standard Atmosphere (ISA). Altimeters and airspeed meters are calibrated against this standard atmosphere, i.e., are designed such that for a standard atmosphere they always would yield correct results. Due to the varying atmospheric conditions, they won’t yield correct results in practice though. For the altimeters, which we use for hiking or biking in the mountains, we know how to deal with this: Whenever we reach a point of known altitude, a hut or a summit, we would readjust the altimeter to indicate the known altitude. We also know that for as long as the weather stays stable, the altimeter will work accurately, but when the weather changes we would guess from our experience and knowledge what difference between indicated and real altitude this would imply. The situation is similar for the altimeter and airspeed meter on the aircraft, and one would typically use alternative data from e.g. a GPS to correct for the changes in the atmospheric conditions with e.g. a Kalman filter. This part is however beyond the scope of this article.
We just briefly summarize the key relationships here; excellent sources are available on the web, like the ones provided in the references below.
Within the troposphere, i.e., up to an altitude of 11 km or to the tropopause, the temperature is described by a constant lapse of -6.5 °C per 1000 m, the air is assumed to be described by the ideal gas law ![]() , and the acceleration of gravity to be constant. This completely describes the ISA.
, and the acceleration of gravity to be constant. This completely describes the ISA.
The ISA in addition defines standard values for pressure, temperature, density, and speed of sound at mean-sea level (MSL), which are ![]() hPa,
hPa, ![]() K,
K, ![]() kg/m
kg/m![]() , and
, and ![]() m/s. The acceleration of gravity is fixed to
m/s. The acceleration of gravity is fixed to ![]() m/s
m/s![]() , the gas constant of air to
, the gas constant of air to ![]() J/kgK, and the heat capacity ratio to
J/kgK, and the heat capacity ratio to ![]() . In the troposphere the lapse is, as mentioned,
. In the troposphere the lapse is, as mentioned, ![]() °C/m.
°C/m.
For the density ratio one immediately obtains from the ideal gas law, that
![]() Eq. (10)
Eq. (10)
It thus seems that the mission of determining ![]() was accomplished easily. However, Eq. (10) is valid only for the ISA, which, as discussed, is rarely met in practice. Thus, corrections need to be made.
was accomplished easily. However, Eq. (10) is valid only for the ISA, which, as discussed, is rarely met in practice. Thus, corrections need to be made.
For completeness, further useful equations are cited:
![]() or
or 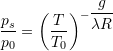 Eq. (11)
Eq. (11)
![]() ,
, 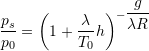 ,
, 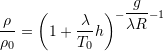 Eqs. (12a), (12b), (12c)
Eqs. (12a), (12b), (12c)
where
![]() ,
, ![]() m
m![]() ,
, ![]() Pa/m Eqs. (13a), (13b), (13c)
Pa/m Eqs. (13a), (13b), (13c)
References I liked:
UC4H Airspeed Node
Design
Results
The firmware currently allows us to measure differential pressure or airspeed, respectively, using the DLHR or RSC sensors, and air temperature using a DS18B20 temperature sensor. The node is in practical testing. An ArduPilot branch with code for using the UC4H Airspeed sensor is here: https://github.com/olliw42/ardupilot/tree/airspeed.
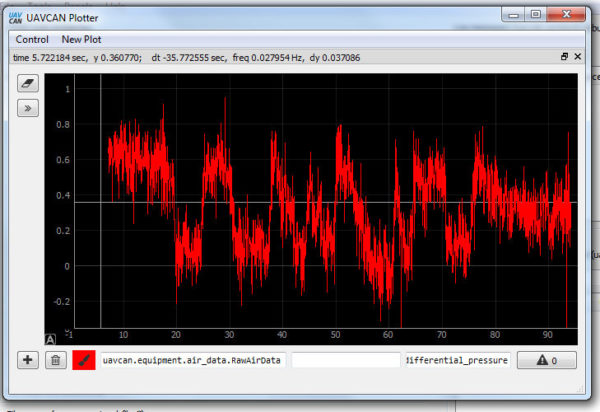
The test results so far look very promising. For instance, the orientational dependence of a RSC ±20 inH2O sensor is only 0.5 Pa, which can be compared to the 8 Pa of the MS5525DSO sensor (reported by kd0aij here). Also, the zero offset appears to be well below ±1 Pa, after auto zeroing.
Further test results can be found here:
- UC4H Airspeed Node, Update
- Differential Pressure Sensors: DLHR vs RSC Comparison II
- Differential Pressure Sensors: DLHR vs RSC Comparison III
Plot of the zero offset and orientational dependence for a RSC sensor with full span of ±5000 Pa: