Im Zuge meiner 4-1+2in1, Koaxgyromixer und GA250 CP-Gyro Projekte habe ich mich recht intensiv mit dem Thema Gyro beschäftigt. Meine Erkenntnisse dazu möchte ich hier darstellen. Ich habe das auch in einem Thread bei RCGroups zusammengeschrieben: The Heli Gyro as a Controller: Theory and Experiment. Für den der es lieber auf English mag ;).
Ich werde hier den Gyro aus der Sicht der Regler betrachten. Was ihr also nicht finden werdet ist eine Beschreibung was ein Gyro ist, wozu er da ist, wie er benutzt wird, wie er eingebaut und eingestellt wird, usw. … dazu gibt es wirklich mehr als aussreichende Informationen auf dem Netz. Ich möchte hier sozusagen einen tiefen Blick in den Gyro hinein wagen, nämlich auf die Regelalgorithmen wie sie in der Firmware verwendet werden. Ich werde allerdings nicht beliebig „tief“ in die Kiste schauen; es geht mir hier (nur) um die grundlegende Reglerstruktur.
Klar, wie die Meisten weiss ich natürlich auch nicht was in den kommerziellen Gyros tatsächlich für Regler implementiert sind. Ich habe beruflich nichts mit Gyros zu tun, und meine einzige Informationsquelle ist das Web. Ich kann also auch nur „raten“, denke aber das wir davon ausgehen können, dass es sich um einen PID-Regler oder einer seiner Varianten handelt. Die Indizien dafür sind „erdrückend“. Zudem finde ich es ja schon immer wieder cool was für hochwertige Infos im Netz zu finden sind (ich rede also nicht von den „üblichen Verdächtigen“ wie die Wikipedia or RN Webseiten). Das was ich hier beschreibe ist das Ergebnis gründlicher Recherche im Netz, und, da es zum Thema Gyros eigentlich wenig bis nichts gibt, eigener Gedanken. Was vom Ergebnis zu halten ist soll jeder für sich entscheiden.
Bevor ich mit der Reglergeschichte ernst mache, möchte ich noch eine Bemerkung vorausschicken:
In den Foren gibt es eine große Anzahl von Threads zu Gyros und FBL Systemen, mit Tipps und Tests. Zum größten Teil „mag“ ich die nicht besonders, denn Schlussfolgerungen werden – meiner Meinung nach – allzu oft nach „mittelalterlichen“ Denkweisen gezogen. Es scheinen mir insbesondere zwei Aspekte zu sein die gerne vermischt werden, nämlich was leistet der Heli bzw. kann er leisten und was leistet der Gyro bzw. kann er leisten. Das charakteristische Beispiel ist das „back bouncing“ nach einem abrupten Stopp, welches zu eine Art Mantra geworden ist. Es gibt IMHO einen einfachen Test um das auseinanderzuhalten:
Test: Vergleiche das Stoppverhalten des Helis mit dem Gyro im Rate- und im Headinghold-Mode.
Im Rate-Mode sieht man (im Wesentlichen) das wozu der Heli in der Lage ist (Heli heisst hier die ganze Mechanik inkl. Servo etc.). Üblicherweise fühlt sich das Heck schön „crisp“ an und zeigt kein „back bouncing“. Beobachtet man im Headinghold-Modus ein anderes (schlechteres) Verhalten… nun, dann liegt das am Gyro und nicht am Heli (oder Servo oder Heck). Bei einem guten Gyro wird man ein ähnlich gutes Stoppverhalten wie im Rate-Mode erreichen. Das Ziel lautet also,
Ziel: Das Heck soll zugleich so „bounce-less“ UND „crisp“ wie möglich sein. Es ist einfach das Eine auf Kosten des Anderen zu erreichen.
Ich betone diesen Punkt so sehr weil das Verhalten des Helis/Gyros bei einem abrupten Stopp im Folgenden eine wichtige Rolle spielen wird. Tatsächlich geht es im Wesentlichen darum zwei eigentlich einfache Sachverhalte aufzuzeigen, die aber irgendwie doch schwer zu akzeptieren zu sein scheinen, jedenfalls gemessen an den Kommentaren in den Foren :):
- Sowohl der Rate- wie auch Headinghold-Gyro basiert auf einem PID-Regler. Der Unterschied zwischen Rate- und Headinghold-Verhalten ergibt sich durch das unterschiedliche Tuning des PID-Reglers.
- Ein auf Headinghold-Verhalten abgestimmter PID-Regler zeigt prinzipbedingt ein starkes „back bouncing“. Dieses kann durch Erweiterungen des PID-Regler abgeschwächt werden.
Dadurch ergibt sich sofort, das viele Aussagen wie sie auch in ansonsten sehr guten Abhandlungen/Erklärungen im RC Bereich zum Gyro, wie z.B. das der I-Term dem Headinghold entspräche oder das das „back bouncing“ durch einen D-Term abzuschwächen sei falsch sind. Mir scheint es da einige Missverständnisse zu geben, die leider zu falschen Aussagen führen. Und mir scheint das auch daran zu liegen, dass die auf den üblichen PID-Webseiten zu findenden Erklärungen zur Bedeutung der PID-Parameter „gedankenlos“ auf den Headinghold-Modus übertragen werden, was aber so nicht geht. Das Anliegen dieses Artikels könnte also auch so formuliert werden, dass er diesen Sachverhalt aufklären will.
Im folgenden Abschnitt werde ich zunächst kurz auf den Rate-Gyro eingehen. Im nächsten Abschnitt wird dann der Headinghold-Gyro „hergeleitet“. Die Probleme beim Headinghold-Gyro und warum er zu „back bouncing“ neigt werden hoffentlich klar. In den anschliessenden Abschnitten wird versucht die Befunde/Aussagen anhand von experimentellen Daten sowie Simulationen zu untermauern bzw. weiter zu veranschaulichen.
Es wird einige Zeit dauern bis ich das alles niedergeschrieben habe, aber das Allermeiste ist wie gesagt bereits in dem oben erwähnten Thread bei RCGroups zu finden, auf den ich deshalb nochmals verweise.
1. Der elementare Rate-Gyro
Wann immer es um Regler geht muss man zuerst die Frage beantworten, was den die Größe ist die man regeln will. Die Antwort ist fast immer offensichtlich. Die Regelgröße bei einem Temperaturregler ist – genau – die Temperatur. Die Regelgröße bei einem Rate-Gyro ist – sehr gut – die Drehrate.
- Der elementare Regler für einen Rate-Gyro ist ein P(ID)-Regler bzgl. der Drehrate.
Tatsächlich reicht meiner Erfahrung nach bereits ein einfacher P-Regler aus um recht gute Flugeigenschaften zu bekommen. Daher habe ich P(ID)-Regler geschrieben, um anzudeuten das mit den I- und D-Anteilen natürlich das Regelverhalten noch weiter verbessert werden kann, diese aber nicht wirklich essentiell sind. Ich persönlich halte den zum Einstellen benötigte Mehraufwand tatsächlich für nicht die Mühe Wert.
Das folgende Bild soll die Situation anschaulicher darstellen, und meine Notation einführen:
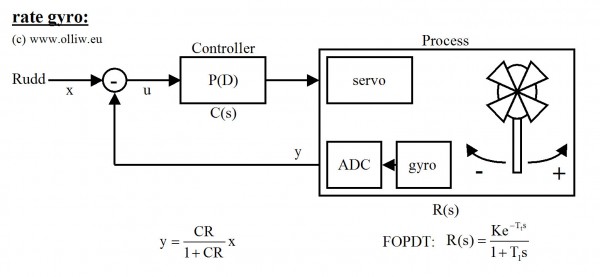
Das Bild sagt eigentlich alles. Ein Punkt möchte ich aber heraustreichen, da er im Folgenden sehr wichtig wird:
- Bezüglich der Drehrate ist der Helikopter eine Regelstrecke mit Ausgleich („self-regulating process“).
Ich möchte hier nicht gross darauf eingehen was das ist; googlen liefert viele ausgezeichnet Texte. Nur ganz kurz, eine Regelstrecke mit Ausgleich ist ein System welches sich nach einer Störung wieder von selbst „einpendelt“ und einen neuen Ruhezustand findet. Im Fall eines Helis heißt das nur, dass der Heli nachdem der Rudder-Knüppel wieder in die Neutralstellung gebracht wurde aufhören wird sich weiter zu drehen. Ist also nicht wirklich spektakulär.
Für eine Regelstrecke mit Ausgleich kommen verschiedene Modelle in Frage. Das einfachste Modell ist eine PT1-Strecke, aber ich werde unten anhand von Experimenten zeigen das eine Heli (bzw. mein Heli) nicht als PT1-Prozess beschrieben werden kann. Eine gewisse Verzögerung und/oder Totzeit ist vorhanden, was auf das PT2 und/oder FOPDT-Modell hinweist, aber ein PT2-Model wird sich auch als nicht ausreichend erweisen. Das einfachste für einen Heli geeignet Model ist also das FOPDT-Modell. Dieses Modell ist nebenbei bemerkt auch das üblicherweise benutzte Modell für Regelstrecken mit Ausgleich, und eigentlich alle bekannten Tunningregeln sind für dieses Modell gemacht (jeder von Euch hat vermutlich von Ziegler Nichols oder einer der Varianten gehört).
- Bezüglich der Drehrate stellt das FOPDT-Modell das einfachste Modell für einen Helikopter dar.
Das FOPDT-Modell ist natürlich nur das allereinfachste Modell. Tatsächlich beobachte ich bei meinem Heli Verhaltensweisen die damit nicht ganz richtig beschrieben werden. Meine experimentellen Möglichkeiten reichen nicht aus um ein genaueres Modell zu erstellen. Aber eigentlich will ich das auch gar nicht, denn es ändert nichts an den grundsätzlichen Aussagen, und nur auf diese kommt es mir an. Das heisst, wir nehmen die Einschränkungen des FOPDT-Modells zur Kenntnis, sind aber ansonsten glücklich damit.
2. Der elementare Headinghold-Gyro
2.1. „Herleitung“ der Headinghold-Reglerstruktur
Wie zuvor für den Rategyro stellt sich als Erstes die Frage, welche Größe den zu Regeln ist. Für den HH-Gyro scheint die Antwort weniger offensichtlich zu sein, zumindest führt bereits dieser Punkt in Forendiskussionen zu Kontroversen. Betrachten wir das zunächst etwas genauer.
Nun, was erwarten wir eigentlich für ein Verhalten von einem Heli mit HH-Gyro? Klar, der Heli soll stur seine Richtung bei behalten, passiere was da wolle. Richtung bedeutet aber nichts anders als Winkel. Ein Beispiel dazu: Bei einem plötzlichen Pitchstoß möchte das Heck ausschlagen, d.h., der Heli möchte sich drehen. Ein Rategyro versucht nun die Drehung zu stoppen und wird dies auch erreichen, aber das Heck hat sich derweil ein bischen nach rechts bewegt. Der Rategyro kann diese Richungsänderung nicht korrigieren, da der Heli sich ja nun nicht mehr dreht; er hat sein Ziel erreicht und die Drehung des Hecks unterbunden. Bei einem HH-Gyro soll der Gyro das Heck auch wieder zurück in die Ausgangslage bringen, d.h. wir erwarten nicht nur, dass der Gyro die Drehung zum stoppen bringt, sondern das er zunächst eine entgegengsetzte Drehung erzwingt und erst wenn die urprüngliche Richtung wieder erreicht ist die Drehung stoppt. Ein HH-Gyro kann also offensichtlich kein Regler bzgl. der Drehrate sein. Er ist ein Regler bzgl. der absoluten Richtung bzw. des Drehwinkels.
- Der elementare Regler für einen Headinghold-Gyro is ein P(I)D Regler bzgl. dem Drehwinkel.
Technisch erhalten wir den Drehwinkel aus dem Signal des Gyrosensors durch Integration des Selbigen (der Gyrosensor misst die Drehrate, und das Integral liefert den absoluten Drehwinkel).
Es gibt nun allerdings ein „kleines“ Problem. Würden wir einfach einen Regler für das integrierte Gyrosensor-Signal aufbauen, dann würde mit dem Rudder-Knüppel der absolute Winkel des Helis kontrolliert werden. Diese Betriebsarte findet sich manchmal bei Multikoptern. Beim Heli wollen wir das aber sicher nicht, hier wollen wir mit dem Rudder-Knüppel die Änderung des Winkels bzw. der Richtung kontrollieren. Um das zu erreichen müssen wir auch das Rudder-Signal integerieren, und das integrierte Signal in den Regler einspeisen. Auf diese Weise erhält man einen Regler, welcher versucht den Winkel = Richtung des Helis bei Störungen beizubehalten, während mit dem Rudder-Knüppel die Drehrate gesteuert wird, also genau dass was wir wollen. Der resultierende Regler sieht schematisch wie folgt aus:
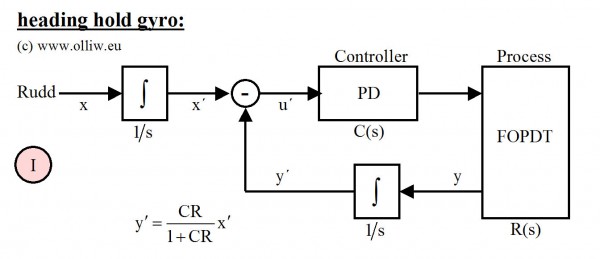
Im Prinzip war es das bereits :). Ich finde es jedoch sehr einsichtsfördernd die erhaltene Reglerstruktur (I) noch weiter zu analysieren. Im Folgenden benutze ich einen einfachen (mathematischen) Trick: In einer geschlossenen Schleife kann ein Block an eine andere Stelle in der Schleife „verschoben“ werden solange einige Regeln beachtet werden (auf diese Regeln gehe ich hier nicht weiter ein, diese finden sich in jedem Regler-Lehrbuch, bitte benutzt google). Entscheidend ist, dass die so erhaltenen alternativen Regelstrukturen absolut äquivalent zu der Urprünglichen sind.
2.2. Eine für die Implementierung geeignete Headinghold-Reglerstruktur
Die soeben dargestellte Reglerstruktur (I) ist so nicht für eine praktische Implementierung geeignet. Wegen der Integrationen müsste man sorgfältig auf Überläufe des Winkels achten. Glücklicherweise lässt sich das leicht durch einen Trick vermeiden: Die zwei Integralboxen im obigen Schema, welche sich vor der „-“ Box befinden, können zusammengefasst und hinter die „-“ Box verschoben werden. Auf diese Weise wird nur noch die Differenz zwischen den Winkelsignalen vom Rudder und dem Gyrosensor betrachtet (u‘ = y‘ – w‘ im obigen Bild), welche unter normalen Umständen immer klein bleibt. Die resultierende Reglerstruktur (II) habe ich wieder in einem Bild skizziert:
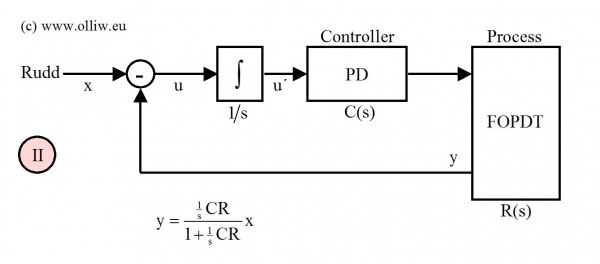
Wenn wir aber mal soweit sind, dann können wir weiter „tricksen“ und die Reglerstrukturen (III) und (IV) erhalten. Der Trick besteht einfach darin, die Integralbox (also das 1/s) entweder im Regler (Struktur III) oder in der Regelstrecke (Struktur IV) zu absorbieren. Es soll nochmals betont werden, dass alle diese Reglerstrukturen absolut gleichwertig zur ursprünglichen Struktur (I) sind. Von der theoretischen/mathematischen Seite her ist es also egal welche man betrachtet, d.h., wir können uns die unserer Meinung nach für eine bestimmte Überlegung am Besten geeignete Struktur frei aussuchen.
Betrachten wir zunächst die unten abgebildte Strukur (III). Hier wurde die Integralbox im Reglerblock absorbiert. Das Resultat ist lustig, denn der ursprüngliche PD-Regler wird dadurch in einen PI-Regler verwandelt:
ursprünglicher Regler: C(s) = P + Ds
„neuer“ Regler: C'(s) = 1/s * C(s) = P/s + D = I’/s + P‘
Aus der Sicht der Reglertheorie betrachtet entspricht also der I-Anteil des implementierten Reglers (I‘) tatsächlich einem P-Term, und der P-Anteil (P‘) entspricht einem D-Term.
- Bezüglich der Drehrate stellt der Headinghold-Gyro einen PI-Regler dar, wobei der I-Parameter die Funktion des P-Anteils einnimmt, und der P-Parameter die des D-Anteils.
Das klingt ja verrückt. Das klingt genauso wie mathematische Tricks eben klingen. Nichtsdestotrotz, meiner Meinung nach ist das vielleicht die entscheidende Feststellung, und im Folgenden geht es „nur noch“ darum die Bedeutung und Konsequenzen klarer darzustellen. Wie auch immer, die Reglerstruktur (III) ist offensichtlich die für die Implementierung geeignete; einen PID-Regler zu programmieren ist kein großes Geheimis und Standard.
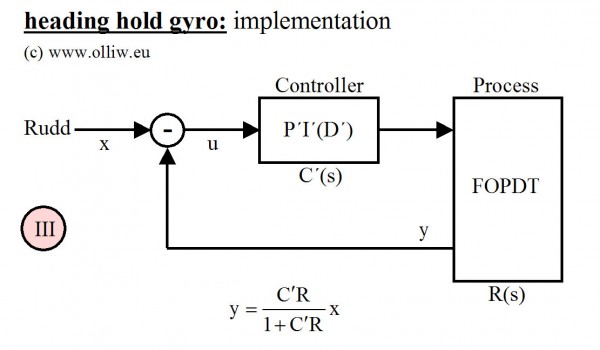
Ich möchte nochmal auf die etwas „mysteriöse“ Logik in dem Ganzen eingehen. Jeder hätte vermutlich von vorneherein einen PID-Regler bzgl. der Drehrate benutzt, während ich jetzt hier ein großes „Gedöns“ veranstaltet habe nur um (scheinbar) auf genau das Ergebnis zu kommen. Was sollte das Ganze also? Nun, es geht darum, wie die PID Parameter einzustellen sind:
- Ob man einen Rategyro oder Headinghold-Gyro erhält, hängt vom Tuning der PI(D) Parameter ab.
Es geht also um die Interpretation bzw. Auswirkung der Parameter des implementierten PID-Reglers (d.h. diese lustige I ist P und P ist D Aussage), und es geht um die geeigneten Tunningregeln oder Strategien.
2.3. Eine für das Verständnis des Headinghold-Gyros geeignete Reglerstruktur
Mit einem ähnlichen Trick wie eben kommt man im Verständis einen erheblichen Schritt weiter: Absorbiert man die Integralbox nicht im Regler sondern in der Regelstrecke erhält man die nachfolgend skizzierte Reglerstruktur (IV):
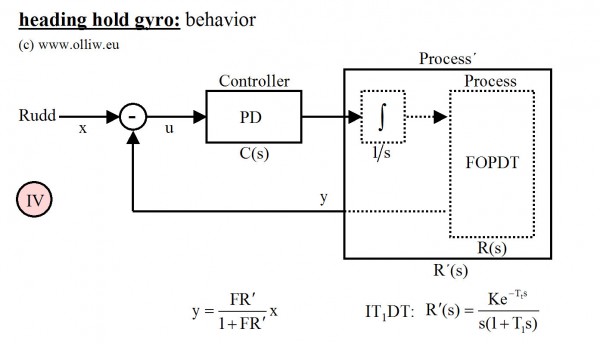
Hier wird also nicht der Regler verändert, es handelt sich nach wie vor um den selben PD-Regler wie in der ursprünglichen Struktur (I), und die P und D Parameter entsprechen genau dem Gewohnten und in jedem Standardtext zum Regler beschriebenen. Aber, und das ist nun entscheidend, die Regelstrecke hat sich verändert. Es handelt sich nun nicht mehr um eine Strecke mit Ausgleich, wie beim Rategyro oder den anderen obigen Reglerstrukturen, sondern um eine sogenannte Strecke ohne Ausgleich oder integrierende Strecke.
- Bezüglich des Drehwinkels ist der Helikopter eine Regelstrecke ohne Ausgleich („integrating process“).
Ich werde hier wieder nicht erklären was eine integrierende Strecke ist, bitte googeln. Aber diese Beoachtung is der springende Punkt. Genauso wie für die Strecke mit Ausgleich gilt auch für die Strecke ohne Ausgleich, dass es verschiedene Modelle zur Beschreibung gibt. Das einfachste Modell ist eine I-Strecke, aber diese taugt nicht zur Beschreibung eines Helikopters da die Delay- und/oder Totzeiten wieder nicht angemessen berücksichtigt sind. Das verweist auf eine IT1-Strecke als einfachstes geeignetes Modell. Gehen wir allerdings von einem FOPDT-Model für die Regelstrecke bzgl. der Drehrate aus, wie wir es oben taten, erhalten wir ein IT1DT-Modell. Mit den mir zur Verfügung stehende Informationen/Messdaten kann ich nicht klar zwischen diesen beiden Modellen entscheiden.
- Bezüglich des Drehwinkels stellt das IT1- oder IT1DT-Modell das einfachste Modell für einen Helikopter dar.
Welche Bedeutung hat das nun? Es bedeutet z.B. das um die Funktion des Headinghold-Gyros zu verstehen man die Literatur über Strecken ohne Ausgleich und IT1-Strecken insbesondere ansehen muss, und nicht die „übliche“ Literatur welche sich (leider) vorwiegend mit Strecken mit Ausgleich beschäftigen. Weiterhin bedeutet es z.B. auch das um die „beste“ Eisntellung des Reglers zu finden man sich die Tunningregeln für IT1-Strecken ansehen muss, und nicht die „üblichen“ Tunningregeln wie z.B. Ziegler-Nichols and Family welche sich auf Strecken mit Ausgleich beziehen. Tatsächlich sind die Tunningregeln für Strecken ohne Ausgleich deutlich andere; um ein Schlagwort für die google-Suche einzuwerfen: symmetrical optimum. Kurzum, folgt man „naiv“ den in den weitverbreiteten Regler-Webseiten beschrieben Einstellregeln wird man keinen (guten) Headinghold-Gyro erhalten.
Mit diesen Überlegen wird die oben erwähnte “mysteriöse” Logik (hoffentlich) klarer: Sowohl beim Rate- wie auch Headinghold-Gyro wird im Wesentlichen die gleiche Reglerstruktur (PID Regler bzgl. der Drehrate) implementiert, dessen Funktion entscheidet sich jedoch durch die Einstellung der Reglerparameter, I und P. Wird der Regler entsprechend den in den „üblichen“ Artikeln dargelegten Tuningregeln eingestellt, dann erhält man einen perfekt getunten – Rategyro. Wird der Regler jedoch unter Berücksichtung „I entspricht P und P entspricht D“ bzw. den Regeln für Strecken ohne Ausgleich eingestellt erhält man einen Headinghold-Gyro.
Es mag vielleicht aufgefallen sein das ich nicht, wie beim Rategyro, sagte, dass man einen perfekt getunten Headinghold-Gyro erhält. Das Ergebnis des optimalen Tunings wird für einen Helipiloten in der Tat nicht optimal erscheinen da entweder das Heck zu „schwammig“ ist oder ein starkes „back bouncing“ auftritt. Unten werde ich das z.B. anhand von Simulationen weiter veranschaulichen, aber der Grund ist schon hier deutlich: Für den Rate- oder Headinghold-Modus muss der PID-Regler unterschiedlich eingestellt werden, d.h. aber dass wenn die Rate-Einstellregeln ein „perfektes“ Heck ergeben dann kann die Headinghold-Einstellung nicht auch ein prefektes Heck ergeben. Tatsächlich muss der I Parameter für ein gutes Headinghold deutlich größer sein als für den Ratemode, was zu Overshoot und Oszillationen führt, welche man als Backbouncing wahrnimmt.
2.4. Die elementare Headinghold-Reglerstruktur
In der Literatur gibt es ein Standardverfahren (googlen!) um den Overshoot bzw. das Backbouncing zumindest deutlich zu veringeren, nämlich ein Vorfilter in den Rudderzweig einzufügen, wie in dieser Skizze gezeigt:
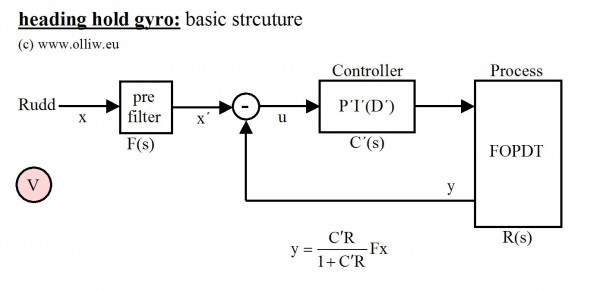
Das Vorfilter kann z.B. ein einfaches T1-Glied (Tiefpass 1. Ordnung) oder ein Accelaration/Decelaration-Begrenzer sein. Es ist hierbei wichtig zu bemerken, dass dieser Block nicht in den Reglerzweig oder den Rückkopplungszweig eingefügt werden darf, da sonst die Reglerperformance beeinträchtigt werden würde. Mit dem Vorfilter kann das Backbouncing unterdrückt werden, aber leider geht das auf Kosten der Responsezeit, und das Heck wird nicht so crisp sein wie es sein könnte, wie z.B. im Ratemode. Es muss hier also, wie so oft im Leben, ein Kompromis eingegangen werden.
2.5. Zusammenfassung
So, das war das was ich zum Prinzip des Headinghold-Gyros sagen wollte. Ich glaube das die Reglerstruktur (V) die geeignete elementare Regelerstruktur für einen Headinghold-Gyro darstellt, und wie meine Experimente zeigen können damit auch recht gute Ergebnisse erzielt werden. Die Struktur hat allerdings eine prinzipbedingte Schwäche dahingehend, dass das Heck nicht so crisp ist, und auch nicht sein kann, wie im Ratemodus. Das liegt meiner Meinung nach aber nicht an der speziellen Struktur (V) sondern ist eine fundamentale Konsequenz der Tatsache, dass der Heli im Headinghold-Modus eine Strecke ohne Ausgleich darstellt. Verbesserungen/Erweiterungen der Struktur (V) drängen sich auf, wie z.B. feed forward oder gain scheduling. Damit kann die Performance des Hecks sicher verbessert werden, aber das grundsätzliche Problem kann damit nicht (leicht) umgangen werden, und ich denke dass der mögliche Performancegewinn kleiner ausfällt als erhofft.
3. Experiment I
4. Simulationen
5. Experiment II
6. Zusammenfassung
