I. Coordinate Transformation, DCM
![]() : Vector in Euklidian space
: Vector in Euklidian space
![]() : Coordinates of a vector
: Coordinates of a vector ![]() measured in the frame
measured in the frame ![]()
![]() : Coordinates of a vector
: Coordinates of a vector ![]() measured in the frame
measured in the frame ![]()
![]()
![]()
![]()
Coordinates ![]() of basis vector
of basis vector ![]() measured in Frame
measured in Frame ![]() :
:
![]()
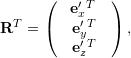
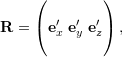
![]()
![]()
![]() :
: ![]() -th coordinate of vector
-th coordinate of vector ![]() measured in K
measured in K
![]() :
: ![]() -th coordinate of vector
-th coordinate of vector ![]() measured in K‘
measured in K‘
Transformation of coordinates of a vector ![]() :
:
![]()
![]()
![]()
II. Rigid Body
![]() : Orientation of body-fixed coordinate frame as measured in the earth coordinate frame
: Orientation of body-fixed coordinate frame as measured in the earth coordinate frame
![]() : Coordinates of a vector
: Coordinates of a vector ![]() measured in the earth frame
measured in the earth frame
![]() : Coordinates of the same vector
: Coordinates of the same vector ![]() measured in the body frame
measured in the body frame
![]() : Rotation rate vector of body measured in the body frame
: Rotation rate vector of body measured in the body frame
![]() : Unit quaternion associated to the rotation matrix
: Unit quaternion associated to the rotation matrix ![]()
![]()
![]()
![]()
Definition Pitch-Roll:
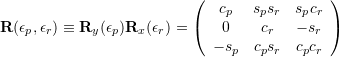
![]()
![]()
Definition Yaw-Pitch-Roll:
![]()
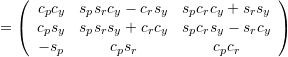
![]()
![]()
Definition II Roll-Pitch:
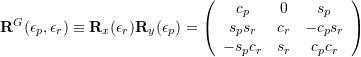
![]()
![]()
Definition II Yaw-Roll-Pitch:
![]()
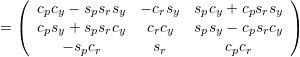
![]()
![]()
III. Rotations
Rotation Matrices
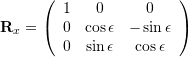
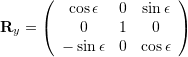
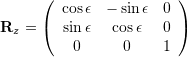
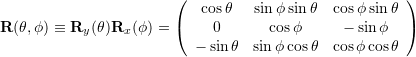
![Rendered by QuickLaTeX.com \begin{array}{rcl} {\bf{R}}(\Psi,\theta,\phi) &\equiv& {\bf{R}}_z(\Psi) {\bf{R}}_y(\theta) {\bf{R}}_x(\phi) \\[9px] &=& \left(\begin{array}{ccc} \cos\theta \cos\Psi & \sin\phi \sin\theta \cos\Psi - \cos\phi \sin\Psi & \cos\phi \sin\theta \cos\Psi + \sin\phi \sin\Psi \\ \cos\theta \sin\Psi & \sin\phi \sin\theta \sin\Psi + \cos\phi \cos\Psi & \cos\phi \sin\theta \sin\Psi - \sin\phi \cos\Psi \\ -\sin\theta & \sin\phi \cos\theta& \cos\phi \cos\theta \end{array}\right) \end{array}](https://www.olliw.eu/wp-content/ql-cache/quicklatex.com-bf3a339f2b62fea893cb6c075a610311_l3.png)
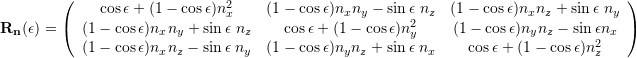
![]()
![]()
![]()
Generators

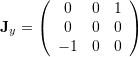
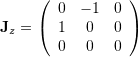
![]()
![]()
Definition: ![]()
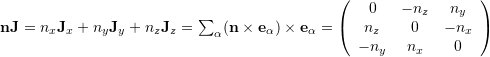
![]()
![]()
![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]()
![]()
Rotations and Generators
![]()
![]()
![]()
Rotation Derivatives
Definition: ![]()
![]()
![]()
![]() ,
, ![]() ,
, ![]()
Skew Symmetric Matrices
![]() ,
, ![]()
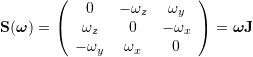
![]()
![]()
Rotations and Skew Symmetric Matrices
![]() ,
, ![]()
![]() ,
, ![]()
![]()
Exponential Map
![]()
![]()
![]() with
with ![]()
![]()
IV. Quaternions
![]() : Quaternion
: Quaternion
![]() : Real part of quaternion
: Real part of quaternion ![]()
![]() : Imaginary part of quaternion
: Imaginary part of quaternion ![]()
![]()
![]()
![]()
![]()
Quaternion Multiplications
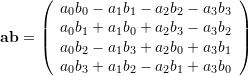
![]()
![]()
![]()
![]()
![]()
Unit Quaternions
![]()
![]()
Unit Quaternions and Rotations
![]() : Unit quaternion associated to the rotation matrix
: Unit quaternion associated to the rotation matrix ![]()
![]() : Rotation matrix
: Rotation matrix ![]() associated to the unit quaternion
associated to the unit quaternion ![]()
![]()
![Rendered by QuickLaTeX.com \begin{array}{rcl} {\bf{R}}|_{\bf{q}} &=& \left(\begin{array}{ccc} q_0^2 + q_1^2 - q_2^2 - q_3^2 & - 2 q_0 q_3 + 2 q_1 q_2 & 2 q_0 q_2 + 2 q_1 q_3 \\ 2 q_0 q_3 + 2 q_1 q_2 & q_0^2 - q_1^2 + q_2^2 - q_3^2 & - 2 q_0 q_1 + 2 q_2 q_3 \\ - 2 q_0 q_2 + 2 q_1 q_3 & 2 q_0 q_1 + 2 q_2 q_3 & q_0^2 - q_1^2 - q_2^2 + q_3^2 \end{array}\right) \\[24px] &=& 2 \left(\begin{array}{ccc} q_0^2 + q_1^2 - \frac{1}{2} & - q_0 q_3 + q_1 q_2 & q_0 q_2 + q_1 q_3 \\ q_0 q_3 + q_1 q_2 & q_0^2 + q_2^2 - \frac{1}{2} & -q_0 q_1 + q_2 q_3 \\ -q_0 q_2 + q_1 q_3 & q_0 q_1 + q_2 q_3 & q_0^2 + q_3^2 - \frac{1}{2} \end{array}\right) \\[24px] &=& \left( 2 q_0^2 - 1 \right) {\bf{1}} + 2 q_0 [\vec{q}]_\times + 2 \vec{q} \vec{q}^T \end{array}](https://www.olliw.eu/wp-content/ql-cache/quicklatex.com-51e7c93d391c7ea3904f5f871fe2e0bd_l3.png)
![]() , where
, where ![]()
![]()
![]() ,
, ![]() where
where ![]() (for rigid body kinetics it’s
(for rigid body kinetics it’s ![]() )
)
![]()
Note: For numerical implementation see [1].
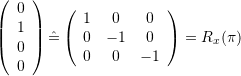
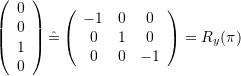
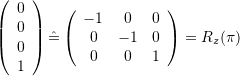
Spherical Linear Interpolation, Slerp
![]() , where
, where ![]()
V. General
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
