Model-based Control
STorM32's model-based gimbal control can take into account, to a certain extend, the non-linear axis couplings and the moments of inertia of the camera and the roll arm. It also allows us to model the different KV values of the pitch, roll and yaw motors.
For the underlying theory see Camera Gimbals: A Robotics Approach.
Parameters
The model used for control is determined by the Foc Controller/Controller parameter in the [GUI:PID] tab, and can assume these settings:
| model | 3 axis (TSTorM32) | 3 axis (w IMU2) | pitch-roll (TSTorM32) | pitch-roll (w IMU2) | pitch-yaw (TSTorM32) | pitch-yaw (w IMU2) |
|---|---|---|---|---|---|---|
| “default” | x | x | - | - | - | - |
| “roll mixing” | x | x | - | - | - | - |
| “mdl based wo roll mix” | x | - | - | - | - | - |
| “model based” | x | - | - | - | - | - |
Gimbal Model Parameters
The model-based control can consider the following parameters.
In the [GUI:PID] tab we see:
- Foc Pitch K, Foc Roll K, Foc Yaw K: Can account for different KV values of the pitch, roll and yaw motors.
In the [GUI:Gimbal Model] tab we see:
- T1 Pitch, T1 Roll, T1 Yaw: Relative moments of inertia of the camera along the pitch, roll and yaw directions.
- T2 Roll, T2 Yaw: Relative moments of inertia of the roll arm along the roll and yaw directions.
Model
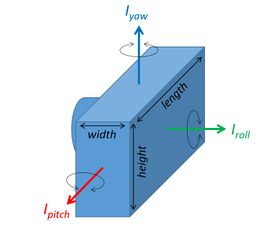
The camera is described by the three principal moments of inertia
- , ,
For illustration see this graphics:
The roll arm is modeled with these moments of inertia
- ,
The yaw arm is not modeled.
In the GUI these moments of inertia can be adjusted via the T parameters, i.e., T1 Pitch sets , T2 Roll sets , and so on.
The model-based PID controller can also take into account different values of the pitch, roll and yaw motors via the K parameters.
Ideal Camera/Gimbal Design
From the perspective of PID control and gimbal axis coupling, these suggestions can be deduced:
Camera
The camera should ideally have these properties:
- or
The first condition is more important than the second, and should be approached if possible.
The second condition suggests a sphere or cube shaped camera, or a long "needle-like" camera with the "needle" along the pitch axis.
Gimbal
For the roll arm a condition , similar to the first condition for the camera, would ideally be fulfilled. This is however almost always unrealistic in practical builds.
Whenever possible, the roll arm should be designed as a U-shaped bracket and not as an L-shaped arm. The U shape brings two benefits: First, the un-modelled non-linearity in the gimbal dynamics is much reduced and the PID controller can work better. Also vibrations in the roll arm limiting the controller performance tend to be lesser.
The yaw arm is a bit of a problem, as it essentially always will have to be of an L-shaped form, bringing in serious gimbal-axis couplings. The situation can be improved by mounting a weight on the roll axis opposite to the camera, e.g. a battery.
Moments of Inertia
Estimates for the relative ratios of the moments of inertia of the camera can be obtained by approximating it by a cuboid.
For a homogeneous solid cuboid holds
Links:
- https://en.wikipedia.org/wiki/Moment_of_inertia
- https://en.wikipedia.org/wiki/List_of_moments_of_inertia
Camera Panasonic
| width | height | length |
|---|---|---|
| 2.5 cm | 5.5 cm | 9 cm |
| axis | approximate moment of inertia | relative ratio |
|---|---|---|
| pitch | I ∝ 2.52 + 5.52 = 36.5 | 1 |
| roll | I ∝ 5.52 + 92 = 111.25 | 3.05 |
| yaw | I ∝ 2.52 + 92 = 87.25 | 2.39 |
Camera GoPro Hero5
| width | height | length |
|---|---|---|
| 2.5 cm | 4.5 cm | 6.3 cm |
| axis | approximate moment of inertia | relative ratio |
|---|---|---|
| pitch | I ∝ 2.52 + 4.52 = 26.5 | 1 |
| roll | I ∝ 4.52 + 6.32 = 59.94 | 2.26 |
| yaw | I ∝ 2.52 + 6.32 = 45.94 | 1.73 |
Camera Mobius
| width | height | length |
|---|---|---|
| 6 cm | 2 cm | 3 cm |
| axis | approximate moment of inertia | relative ratio |
|---|---|---|
| pitch | I ∝ 62 + 22 = 40 | 1 |
| roll | I ∝ 22 + 32 = 13 | 0.325 |
| yaw | I ∝ 62 + 32 = 45 | 1.125 |
As evidenced by these estimates, the shape of the Mobius camera is not ideal from a gimbal control perspective, and this camera is thus more difficult to stabilize than others.