Zum Thema Elektromotor gibt es sehr gute Artikel und Webseiten (meine Favorites: hier). Allerdings, so scheint es mir, sind diese Artikel nicht mit Blick auf Modellhelikopter geschrieben worden. Es werden zwar viele Diagramme und Fälle diskutiert, aber die Heli-Piloten interessierenden Fragen meist nicht. Mal sehen, ob ich das hier ändern kann.
Zur Beschreibung des Motors gehe ich wie üblich von den Motorgleichungen aus, werde deren Herleitung aber nicht erklären (das ist im Netz ausreichend beschrieben), sondern werde sie einfach benutzen. Ich werde allerdings zwei „Neuerungen“ einführen – zumindest habe ich diese so noch nicht gesehen – nämlich das Motormodell des linearen Motors und den Leerlauf-Reduktionsfaktor. Normalerweise wird der Motor natürlich auch eine Last wie z.B. einen Rotor antreiben. Neben den Motoreigenschaften ist also auch deren Verhalten zu beschreiben. Im Prinzip ist das ganz einfach, oder unendlich schwer, je nach Betrachtungspunkt. Rotoren möchte ich hier eigentlich nicht diskutieren, und werde deren Verhalten daher nur kurz angeben. Von größtem Interesse ist natürlich das Zusammenspiel von Motor und Last – und gerade zu diesem Punkt gibt es in Bezug auf Helis im Web quasi nichts zu finden (das ist interesanterweise für Modellflugzeuge anders). Dieses Zusammenspiel für Modellhelis zu beleuchten ist daher das eigentliche Ziel.
Dieser Artikel gliedert sich in aufeinander aufbauende Kapitel, die manchmal viele Formeln enthalten. Wer es damit nicht so hat, kann die entsprechenden Textteile einfach überlesen. Ansonsten habe ich versucht den Text lesbar zu halten und Zusammenhänge anhand von Diagrammen anschaulich zu machen. Wesentliche Befunde werden zudem regelmäßig zusammengefasst.
1. Motorgleichungen
1.1. Linearer Motor, 1.2. Halb-idealer Motor
2. Rotor als Last
3. Motorverhalten bei konstanter Spannung
3.1. Mathematische Beschreibung, 3.2. Motordiagramme, 3.3. Leerlauf-Reduktionsfaktor
4. Motorverhalten bei unterschiedlicher Spannung
4.1. Mathematische Beschreibung, 4.2. Motordiagramme
5. Motor mit Rotor als Last
5.1. Mathematische Beschreibung, 5.2. Leistungs-Drehzahl-Diagramme, 5.3. Getriebe und Ritzelgröße,
1. Motorgleichungen
In den Motorgleichungen treten verschiedene Größen auf, welche in zwei Gruppen fallen: Die Betriebsgrößen Spannung ![]() , Drehzahl
, Drehzahl ![]() , Strom
, Strom ![]() , und Drehmoment
, und Drehmoment ![]() beschreiben den aktuellen Betriebszustand des Motors, während die Motorparameter die Eigenschaften des spezifischen Motors beschreiben. Die Anzahl der nötigen Motorparameter hängt vom Motormodell ab.
beschreiben den aktuellen Betriebszustand des Motors, während die Motorparameter die Eigenschaften des spezifischen Motors beschreiben. Die Anzahl der nötigen Motorparameter hängt vom Motormodell ab.
Bemerkung: Ich unterscheide sprachlich nicht explizit zwischen Winkelgeschwindigkeit ![]() , Drehfrequenz
, Drehfrequenz ![]() und Drehzahl
und Drehzahl ![]() ; ich werde meistens
; ich werde meistens ![]() benutzen, aber immer einfach nur Drehzahl sagen.
benutzen, aber immer einfach nur Drehzahl sagen.
Oft wird der Motor durch Motorkenngrößen wie Leerlaufdrehzahl ![]() , Leerlaufstrom
, Leerlaufstrom ![]() , oder maximale Leistung charakterisiert. Diese Kenngrößen sind jedoch keine unabhängigen Größen, sondern müssen aus dem Motormodell bestimmt werden. Ihre Werte hängen allerdings nicht vom Motormodell ab, und können zur Bestimmung der Motorparameter dienen (wobei Vorsicht walten zu lassen ist).
, oder maximale Leistung charakterisiert. Diese Kenngrößen sind jedoch keine unabhängigen Größen, sondern müssen aus dem Motormodell bestimmt werden. Ihre Werte hängen allerdings nicht vom Motormodell ab, und können zur Bestimmung der Motorparameter dienen (wobei Vorsicht walten zu lassen ist).
Die Motorgleichungen in der wohl mit Abstand am häufigsten benutzten (und im Web zitierten) Form sind
![]() , Gl. (1.1a)
, Gl. (1.1a)
![]() , Gl. (1.1b)
, Gl. (1.1b)
wobei das Verlustdrehmoment ![]() drehzahlabhängig sein kann/darf; oft wird
drehzahlabhängig sein kann/darf; oft wird ![]() angenommen. Sie liefern das einfachste und trotzdem noch realistische Motormodell.
angenommen. Sie liefern das einfachste und trotzdem noch realistische Motormodell.
Elektromotore werden heute fast ausschliesslich mit elektronischen Reglern betrieben. Die hierbei benutzte PWM-Ansteuerung bewirkt zusätzliche, komplizierte Effekte; meine Gedanken dazu finden sich im Artikel Zur PWM Ansteuerung von Elektromotoren. Diese Effekte sind für unseren Zweck hier jedoch nicht wirklich wichtig. Der PWM-Betrieb kann berücksichtigt werden, indem in allen Gleichungen die Spannung ![]() durch die im Mittel am Motor anliegende Spannung
durch die im Mittel am Motor anliegende Spannung ![]() ersetzt wird, wobei
ersetzt wird, wobei ![]() das PWM-Taktverhältnis (duty cycle) bedeutet.
das PWM-Taktverhältnis (duty cycle) bedeutet.
1.1. Linearer Motor
In diesem Modell schreiben sich die Motorgleichungen als
![]() , Gl. (1.2a)
, Gl. (1.2a)
![]() . Gl. (1.2b)
. Gl. (1.2b)
Das Verlustdrehmoment wird also als ![]() angenommen. Zusätzlich werden unterschiedliche elektromotorische Konstanten für Drehmoment und Spannung erlaubt; oft wird aber
angenommen. Zusätzlich werden unterschiedliche elektromotorische Konstanten für Drehmoment und Spannung erlaubt; oft wird aber ![]() gesetzt werden. Dieses Modell bzw. den Begriff „linearer Motor“ habe ich nirgends gefunden, es einzuführen ist aber wie ich finde sehr offensichtlich, denn es ist das allgemeinste Motormodell, welches linear in den Betriebsgrößen ist (lineares Gleichungssystem). Diese Eigenschaft, Linearität, ist sehr nützlich, und erlaubt einige Rechnungen und allgemeine Aussagen (vide infra).
gesetzt werden. Dieses Modell bzw. den Begriff „linearer Motor“ habe ich nirgends gefunden, es einzuführen ist aber wie ich finde sehr offensichtlich, denn es ist das allgemeinste Motormodell, welches linear in den Betriebsgrößen ist (lineares Gleichungssystem). Diese Eigenschaft, Linearität, ist sehr nützlich, und erlaubt einige Rechnungen und allgemeine Aussagen (vide infra).
Das lineare Motormodell umfasst als Speziallfälle die „üblichen“ Modelle, wie z.B. das oben angegebene Standardmodell falls ![]() ist, oder das nachfolgende Modell.
ist, oder das nachfolgende Modell.
Bei Bürstenmotoren sind evtl. die Effekte der Bürsten mit zu berücksichtigen, welche oft durch einen Widerstand ![]() sowie einer zusätzlich abfallenden Spannung
sowie einer zusätzlich abfallenden Spannung ![]() beschrieben werden,
beschrieben werden, ![]() . Das Motormodell ist damit immer noch linear. Bürsteneffekte werden hier nicht weiter berücksichtigt; sie können leicht nachträglich „eingebaut“ werden indem
. Das Motormodell ist damit immer noch linear. Bürsteneffekte werden hier nicht weiter berücksichtigt; sie können leicht nachträglich „eingebaut“ werden indem ![]() als
als ![]() interpretiert und die Spannung
interpretiert und die Spannung ![]() durch
durch ![]() ersetzt wird.
ersetzt wird.
1.2. Halb-idealer Motor
In diesem Modell werden ausser der Joule’sche Wärme alle anderen Verlustmechanismen vernachlässigt (was auch ![]() impliziert).
impliziert).
![]() , Gl. (1.3a)
, Gl. (1.3a)
![]() . Gl. (1.3b)
. Gl. (1.3b)
Für die Leerlaufdrehzahl ![]() und den Leerlaufstrom
und den Leerlaufstrom ![]() gilt dann
gilt dann
![]() ,
, ![]() . Gl. (1.4)
. Gl. (1.4)
Quantitativ gesehen ist das Modell nicht sehr genau, allerdings auch wieder nicht soo schlecht, da im üblichen Betrieb die Drehzahl deutlich kleiner als die Leerlaufdrehzahl und der Strom deutlich größer als der Leerlaufstrom ist. Dieses Modell erlaubt durchaus nützliche Abschätzungen, und vorallem ein gutes qualitatives Verständnis. Es ist daher als Referenz nützlich. Als entscheidender Makel ist zu nennen, dass es keine brauchbaren Resultate für den Wirkungsgrad liefern kann.
Bemerkung: Die elektromotorische Konstante ![]() (oder
(oder ![]() ) hängt reziprok mit dem KV-Wert des Motors zusammen:
) hängt reziprok mit dem KV-Wert des Motors zusammen: ![]() .
.
2. Rotor als Last
Aus Sicht des Motors bedeutet eine Last, das er ein (mechanisches) Drehmoment aufbringen muss. Das heißt umgekehrt, für unsere Diskussion ist es ausreichend die Last als ein, im Allgemeinen drehzahlabhängiges, Lastdrehmoment ![]() zu beschreiben. Es ist allerdings praktischer anstatt des Drehmoments die Leistung zu betrachten. Glücklicherweise besteht zwischen Beiden ein einfacher Zusammenhang; für mechanische Leistung und mechanisches Drehmoment gilt ganz allgemein
zu beschreiben. Es ist allerdings praktischer anstatt des Drehmoments die Leistung zu betrachten. Glücklicherweise besteht zwischen Beiden ein einfacher Zusammenhang; für mechanische Leistung und mechanisches Drehmoment gilt ganz allgemein
![]() . Gl. (2.1)
. Gl. (2.1)
Auf die Last bezogen wird diese also durch die Leistung ![]() beschrieben.
beschrieben.
Für einen Rotor ergibt sich in der Beiwert-Theorie für die mechanische Leistung, welche zum Drehen des Rotors aufzuwenden ist, der Zusammenhang
![]() .
. ![]() , Gl. (2.2)
, Gl. (2.2)
wobei die Größe ![]() abkürzend für den Vorfaktor eingeführt wurde.
abkürzend für den Vorfaktor eingeführt wurde. ![]() ist der Leistungsbeiwert,
ist der Leistungsbeiwert, ![]() der Rotorduchmesser, und
der Rotorduchmesser, und ![]() die Luftdichte. In diesem Modell steigt die Leistung kubisch mit der Drehzahl an. Häufig verhält sich der Rotor nicht so ideal wie in der Beiwert-Theorie, und die Leistung wird besser beschrieben durch
die Luftdichte. In diesem Modell steigt die Leistung kubisch mit der Drehzahl an. Häufig verhält sich der Rotor nicht so ideal wie in der Beiwert-Theorie, und die Leistung wird besser beschrieben durch
![]() , Gl. (2.3)
, Gl. (2.3)
wobei der Exponent etwas vom Idealwert 3 abweicht (und der Faktor ![]() ein phänomenologischer Parameter wird).
ein phänomenologischer Parameter wird).
Zwischen erzeugtem Standschub ![]() und aufzuwendender mechanischen Leistung
und aufzuwendender mechanischen Leistung ![]() besteht die Beziehung
besteht die Beziehung
![]() ,
, ![]() , Gl. (2.4)
, Gl. (2.4)
wobei ![]() den Wirkungsgrad des Rotors beschreibt, und nach H. Schenk typischerweise Werte von 0.5 – 0.7 annimmt. Die Gl. (2.4) ist sehr nützlich, denn wenn man einfach ad hoc
den Wirkungsgrad des Rotors beschreibt, und nach H. Schenk typischerweise Werte von 0.5 – 0.7 annimmt. Die Gl. (2.4) ist sehr nützlich, denn wenn man einfach ad hoc ![]() annimmt erlaubt sie eine erste Abschätzung der benötigten Leistung bzw. des gelieferten Schubs.
annimmt erlaubt sie eine erste Abschätzung der benötigten Leistung bzw. des gelieferten Schubs.
Die obigen Formeln beschreiben einen gegebenen Rotor, mit festem Pitch, wie z.B. bei FP-Helis, Flugzeugen oder Multicoptern. Bei CP-Helis ist noch die Abhängigkeit vom Pitchwinkel, ![]() , zu berücksichtigen. Mit dem Pitch ändert sich sowohl der Leistungsbeiwert wie der Wirkungsgrad. Der genaue Verlauf ist nicht gerade einfach, aber beide nehmen tendenziell mit zunehmenden Pitch zu (bis zum Stall, den wir hier nicht betrachten). Für uns reicht es zu wissen, dass der Beiwert bzw. die Größe
, zu berücksichtigen. Mit dem Pitch ändert sich sowohl der Leistungsbeiwert wie der Wirkungsgrad. Der genaue Verlauf ist nicht gerade einfach, aber beide nehmen tendenziell mit zunehmenden Pitch zu (bis zum Stall, den wir hier nicht betrachten). Für uns reicht es zu wissen, dass der Beiwert bzw. die Größe ![]() mit dem Betrag des Pitches zunimmt. Die einfachste Näherung wäre
mit dem Betrag des Pitches zunimmt. Die einfachste Näherung wäre
![]() , Gl. (2.5)
, Gl. (2.5)
Ein Heli besteht nun nicht nur aus einem Rotor und Motor. Bei Flugzeugen oder Multicoptern, bei dennen Rotoren und Motoren direkt verbunden sind, mögen die nach Gl. (2.4) berechneten Leistungen gut mit der Wirklichkeit passen, aber beim Heli kommen alle möglichen „Verbraucher“ hinzu, wie Paddelstangen, Heckrotoren, Getriebe, usw.. Tatsächlich ergibt sich ein recht „trauriges“ Bild. Ein Beispiel:
Effizienz beim TRex 450: Nimmt man D = 71 cm und ein Gewicht von 900 g, dann ergibt sich die für’s Schweben benötigte Leistung, ohne Verluste, zu 27 W. Bei meinem TRex 450 beträgt die Schwebeleistung aber eher 160 W (hier). C. Jung hat für seinen TRex ca. 130 W gefunden (hier). Sagen wir also mal 140 W. Das entspricht einem Wirkungsgrad von 20%! D.h. gerade einmal 1/5 der aufgewendeten elektrischen Leistung gehen ins Schweben.
Das Wissen um die Rotoreigenschaften alleine nützt uns also gar nicht so viel. Man könnte versuchen, die Verluste genauer aufzuschlüsseln. Man würde einen Anteil proportional zur Drehzahl aufgrund z.B. von Reibungsverlusten oder einen Anteil kubisch zur Drehzahl aufgrund z.B. des Heckrotors finden, usw.. Mir sind dazu aber keine Ergebnisse bekannt. Wir werden also keine präzise Formel in die Hand bekommen, um die Frage, wie die vom Motor zu liefernde mechanische Leistung und die Rotordrehzahl zusammenhängen, zu beantwort. Aber wir können versuchen die Tendenz sinnvoll zu beschreiben.
Wir können Gl. (2.3) nämlich auch einfach als phänomenologischen Zusammenhang zur Beschreibung des mechanischen Leistungsbedarfs des Helis, inkl. Heckrotor usw., für verschiedene Drehzahlen verwenden. Die Größe ![]() verliert dann ihre Bedeutung als “Beiwert” des Rotors, und
verliert dann ihre Bedeutung als “Beiwert” des Rotors, und ![]() und
und ![]() sind phenomenologische Parameter, aber Gl. (2.3) ist leistungsfähig genug um Trends gut zu beschreiben.
sind phenomenologische Parameter, aber Gl. (2.3) ist leistungsfähig genug um Trends gut zu beschreiben.
3. Motorverhalten bei konstanter Spannung
Da für den Motor die Last ein drehzahlabhängiges Drehmoment darstellt, erscheint es natürlich, für die Diskussion des Motorverhaltens das Drehmoment-Drehzahl Diagram ![]() heran zu ziehen. Nehmen wir die Spannung als gegeben an, dann kann der Strom aus den Motorgleichungen eliminiert werden, und das Motorverhalten lässt sich als Kurvenschar im
heran zu ziehen. Nehmen wir die Spannung als gegeben an, dann kann der Strom aus den Motorgleichungen eliminiert werden, und das Motorverhalten lässt sich als Kurvenschar im ![]() Diagram darstellen, wobei jeder Kurve einer Spannung
Diagram darstellen, wobei jeder Kurve einer Spannung ![]() zugeordnet ist. Anstatt des Drehmoments finde ich es einsichtiger die Leistung zu diskutieren, und sich die Kurvenschar im Leistungs-Drehzahl Diagram
zugeordnet ist. Anstatt des Drehmoments finde ich es einsichtiger die Leistung zu diskutieren, und sich die Kurvenschar im Leistungs-Drehzahl Diagram ![]() zu betrachten. In diesem Kapitel wollen wir uns zunächst nur den Fall einer konstanten, gegebenen Spannung
zu betrachten. In diesem Kapitel wollen wir uns zunächst nur den Fall einer konstanten, gegebenen Spannung ![]() ansehen; die Kurvenschar für verschiedene Spannungen betrachten wir dann im Kapitel 4.
ansehen; die Kurvenschar für verschiedene Spannungen betrachten wir dann im Kapitel 4.
3.1. Mathematische Beschreibung
Aber zunächst ein paar Formeln. Es ist nützlich die beiden Kenngrößen Leerlaufdrehzahl ![]() und Leerlaufstrom
und Leerlaufstrom ![]() zu benutzen. Für diese ergibt sich
zu benutzen. Für diese ergibt sich
![]() ,
, ![]() , Gl. (3.1)
, Gl. (3.1)
wobei die Abkürzung
![]() , Gl. (3.2)
, Gl. (3.2)
benutzt wurde. Bezogen auf die Spannung ![]() lassen sich weitere Kenngrößen definieren,
lassen sich weitere Kenngrößen definieren,
![]() ,
, ![]() ,
, ![]() ,
, ![]() . Gl. (3.3)
. Gl. (3.3)
wobei ![]() die Leerlaufdrehzahl nur aufgrund der elektromotorischen Konstante
die Leerlaufdrehzahl nur aufgrund der elektromotorischen Konstante ![]() (wie beim halb-idealen Motor) und
(wie beim halb-idealen Motor) und ![]() der Kurzschlussstrom ist (beide können nicht bzw. schwer direkt gemessen werden). Die „Leerlaufkonstante“
der Kurzschlussstrom ist (beide können nicht bzw. schwer direkt gemessen werden). Die „Leerlaufkonstante“ ![]() entspricht dem KV-Wert des Motors wie er mit den üblichen Methoden bestimmt wird, und
entspricht dem KV-Wert des Motors wie er mit den üblichen Methoden bestimmt wird, und ![]() drückt die mechanischen Verluste als elektrischen Widerstand aus. Zusätzlich führe ich noch die Leerlauf-Reduktion
drückt die mechanischen Verluste als elektrischen Widerstand aus. Zusätzlich führe ich noch die Leerlauf-Reduktion ![]() über
über
![]() Gl. (3.4)
Gl. (3.4)
ein, mit den Zusammenhängen
![]() . Gl. (3.5)
. Gl. (3.5)
Der Parameter ![]() gibt anschaulich an, um wieviel Prozent die tatsächliche Leerlaufdrehzahl aufgrund der Verluste niedriger ist als im Idealfall erwartet, und wird sich als eine äußerst nützliche Kenngröße erweisen. Typischerweise wird der Wert im Prozentbereich liegen.
gibt anschaulich an, um wieviel Prozent die tatsächliche Leerlaufdrehzahl aufgrund der Verluste niedriger ist als im Idealfall erwartet, und wird sich als eine äußerst nützliche Kenngröße erweisen. Typischerweise wird der Wert im Prozentbereich liegen.
Mit diesen Kenngrößen und ein bischen Rechenarbeit erhält man für die abgegebene mechanische Leistung ![]() des Motor die Beziehung
des Motor die Beziehung
![]() . Gl. (3.6)
. Gl. (3.6)
Die mechanische Leistung ist also bei ![]() (Stillstand) und
(Stillstand) und ![]() (Leerlauf) gleich Null, und nimmt bei
(Leerlauf) gleich Null, und nimmt bei ![]() (halbe Leerlaufdrehzahl) den maximalen Wert an. Die maximale mechanische Leistung berechnet sich zu
(halbe Leerlaufdrehzahl) den maximalen Wert an. Die maximale mechanische Leistung berechnet sich zu
![]() , Gl. (3.7)
, Gl. (3.7)
Für die aufzubringende elektrische Leistung ![]() ergibt sich die Beziehung
ergibt sich die Beziehung
![]() . Gl. (3.8)
. Gl. (3.8)
Die elektrische Leistung ist also bei ![]() am Größten, nimmt linear mit zunehmender Drehzahl ab, um bei der Leerlaufdrehzahl ihren kleinsten Wert zu erreichen. Für die maximale und minimale elektrische Leistung ergibt sich
am Größten, nimmt linear mit zunehmender Drehzahl ab, um bei der Leerlaufdrehzahl ihren kleinsten Wert zu erreichen. Für die maximale und minimale elektrische Leistung ergibt sich
![]() ,
, ![]() . Gl. (3.9)
. Gl. (3.9)
Die maximale elektrische Leistung hängt dabei nur vom Widerstand (und der Spannung) ab. Für den Wirkungsgrad ![]() erhält man
erhält man
![]() , Gl. (3.10)
, Gl. (3.10)
welcher seinen maximalen Wert ![]() bei der Drehzahl
bei der Drehzahl ![]() annimmt:
annimmt:
![]() ,
, ![]() . Gl. (3.11)
. Gl. (3.11)
Für eine anschauliche Diskussion ist es nützlich, sich auf den halb-idealen Motor als Referenzpunkt zu beziehen. Für diesen ergibt sich qualitativ das selbe Verhalten wie für den linearen Motor, allerdings mit einfacheren quantitativen Resultaten: Die maximale mechanische Leistung ist ![]() , die maximale elektrische Leistung ist
, die maximale elektrische Leistung ist ![]() , die minmale elektrische Leistung ist Null, und der Wirkungsgrad ist
, die minmale elektrische Leistung ist Null, und der Wirkungsgrad ist ![]() . Vergleicht man diese Ergebnisse mit denen von oben, dann findet man für den linearen Motor die intuitiv einsichtigen Beziehungen
. Vergleicht man diese Ergebnisse mit denen von oben, dann findet man für den linearen Motor die intuitiv einsichtigen Beziehungen
![]() ,
, ![]() ,
, ![]() ,
, ![]() . Gl. (3.12)
. Gl. (3.12)
Zusammenfassung der wichtigsten Punkte zum Motorverhalten
- Die gelieferte mechanische Leistung ist bei Stillstand und im Leerlauf gleich Null, und nimmt genau bei der Hälfte der Leerlaufdrehzahl den größten Wert an.
- Die aufzuwendende elektrische Leistung ist bei Stillstand am Größten, nimmt mit zunehmender Drehzahl linear ab, und erreicht bei der Leerlaufdrehzahl ihren kleinsten Wert.
- Die maximal mögliche mechanische Leistung ist kleiner, und die minimal notwendige elektrische Leistung ist größer als im Idealfall. Im Stillstand hängt die elektrische Leistung nur vom Widerstand ab.
- Der Wirkungsgrad ist immer kleiner als das Verhältnis der tatsächlichen Drehzahl zur idealen Leerlaufdrahzahl.
Bevor wir weiter gehen, möchte ich noch kurz auf das Motorverhalten als Funktion des Stroms eingehen. Wie oben ausgeführt erscheint mir die Diskussion mittels der Drehzahl-Diagramme sinnvoller, aber häufig findet man auch die Darstellung als Strom-Diagramme. Die Umrechnung von Drehzahl in Strom gelingt mittels der Beziehung ![]() , und es ergibt sich
, und es ergibt sich
![]() ,
, ![]() . Gl. (3.13)
. Gl. (3.13)
![]() , Gl. (3.14)
, Gl. (3.14)
![]() ,
, ![]() . Gl. (3.15)
. Gl. (3.15)
3.2. Motordiagramme
Es wird vielleicht aufgefallen sein, dass ich die Formeln für die Leistungen Gln. (3.6-3.9) jeweils auch in Einheiten von ![]() angegeben habe. Das ist für eine anschauliche Diskussion des Motorverhaltens, zu der wir nun endlich kommen, hilfreich.
angegeben habe. Das ist für eine anschauliche Diskussion des Motorverhaltens, zu der wir nun endlich kommen, hilfreich.
Im nachstehenden Diagram ist die abgegebene mechanische und aufzuwendende elektrische Leistung als Funktion der Drehzahl dargestellt. Die roten Kurven geben das Verhalten eines linearen Motors wieder (mit ![]() ), und die gestrichelten blauen Kurven das eines halb-idealen Motors zum Vergleich. Alle wesentlichen Eigenschaften sind zu erkennen: Die elektrische Leistung ist im Stillstand durch
), und die gestrichelten blauen Kurven das eines halb-idealen Motors zum Vergleich. Alle wesentlichen Eigenschaften sind zu erkennen: Die elektrische Leistung ist im Stillstand durch ![]() gegeben, und nimmt linear mit zunehmender Drehzahl bis auf den Wert
gegeben, und nimmt linear mit zunehmender Drehzahl bis auf den Wert ![]() im Leerlauf ab. Diese Kurve liegt für jeden realen Motor immer oberhalb der Geraden für den halb-idealen Motor. Die mechanische Leistung ist im Stillstand und im Leerlauf Null, und durchläuft ansonsten eine „Glockenkurve“ (Parabel) mit dem maximalen Wert bei genau der Hälfte der Leerlaufdrehzahl. Diese Kurve liegt für jeden realen Motor immer unterhalb der Kurve für den halb-idealen Motor.
im Leerlauf ab. Diese Kurve liegt für jeden realen Motor immer oberhalb der Geraden für den halb-idealen Motor. Die mechanische Leistung ist im Stillstand und im Leerlauf Null, und durchläuft ansonsten eine „Glockenkurve“ (Parabel) mit dem maximalen Wert bei genau der Hälfte der Leerlaufdrehzahl. Diese Kurve liegt für jeden realen Motor immer unterhalb der Kurve für den halb-idealen Motor.
Es macht also keinen Sinn, den Motor mit einer Drehzahl kleiner als die halbe Leerlaufdrehzahl zu betreiben, da hier für die selbe mechanische Leistung viel mehr elektrische Leistung verbratet wird. Anders gesagt, der Wirkungsgrad ist unnötig schlecht. Der Verlauf des Wirkungsgrads läßt sich tatsächlich gut aus dem Diagram ablesen, ist er doch das Verhältnis von meachnischer zu elektrischer Leistung. Einfach gesprochen, je größer der Unterschied zwischen den zwei Kurven für die mechanische und elektrische Leistung ist, desto schlechter ist der Wirkungsgrad. Diese Betrachtung macht sofort klar, dass bei kleinen Drehzahlen der Wirkungsgrad sicher ziemlich schlecht sein wird. Der Drehzahlbereich in dem vernünftige Wirkungsgrade erreicht werden liegt oberhalb der halben Leerlaufdrehzahl. Bei genau der halben Leerlaufdrehzahl wird, wie das Bild zeigt, der Wirkungsgrad für jeden realen Motor immer kleiner als 50% sein. Leider ist dies aber genau der Punkt, an dem der Motor seine maximale mechanische Leistung liefern kann. Das heißt, es macht auch keinen Sinn dem Motor (dauerhaft) seine maximal mögliche Leistung abzuverlangen. Bei hohen Drehzahlen nahe der Leerlaufdrehzahl ist der Wirkungsgrad auch schlecht, da hier in jedem Fall mindestens die elektrische Leistung ![]() aufzuwenden ist, aber die abgegebene mechanische Leistung sehr klein ist. Wir schliessen: der Drehzahlbereich, in dem der optimale Wirkungsgrad erreicht wird, liegt irgendwo zwischen der halben und der vollen Leerlaufdrehzahl. Als grobe aber nützliche Faustregel kann man sich merken, dass er typisch bei etwa 80-90% der Leerlaufdrehzahl liegt.
aufzuwenden ist, aber die abgegebene mechanische Leistung sehr klein ist. Wir schliessen: der Drehzahlbereich, in dem der optimale Wirkungsgrad erreicht wird, liegt irgendwo zwischen der halben und der vollen Leerlaufdrehzahl. Als grobe aber nützliche Faustregel kann man sich merken, dass er typisch bei etwa 80-90% der Leerlaufdrehzahl liegt.
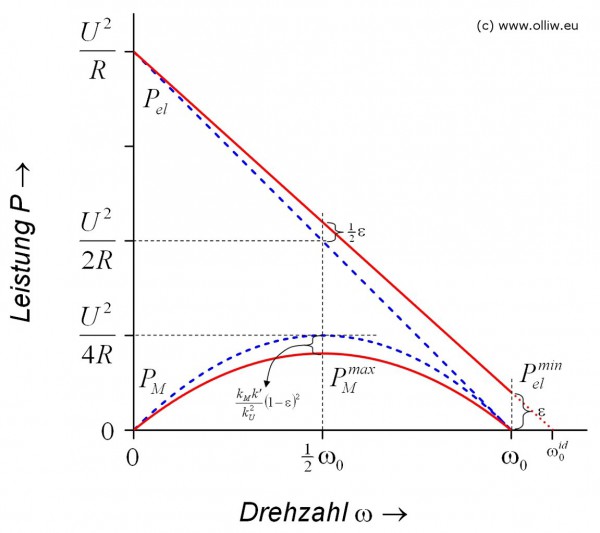
Diese qualitativen Betrachtungen zum Wirkungsgrad werden im folgenden Bild, welches den Wirkungsgrad als Funktion der Drehzahl für den linearen und halb-idealen Motor in rot und blau darstellt, bestätigt. Es ist aber auch zu sehen, dass der gewählte Beispielmotor (![]() ) sehr schlecht ist; der maximale Wirkungsgrad beträgt nicht mal 50%. Das war Absicht, da sonst der Unterschied zwischen dem linearen und halb-idealen Motor in den Diagrammen kaum sichtbar gewesen wäre. Es ist einsichtig, dass bei einem besseren Motor nicht nur der maximale Wirkungsgrad größer wäre, sondern auch die Drehzahl, bei der dieses Maximum erreicht wird. Anschaulich gesagt wandert der roten Punkt nicht nur nach oben sondern auch nach rechts hin zu größeren Drehzahlen. Ein besserer Wirkungsgrad ist natürlich erwünscht, allerdings läßt sich der Vorteil nicht immer voll nutzen. Zum Einen wird die „Spitze“ der Wirkungsgradkurve spitzer, und der nutzbare Drehzahlbereich, in dem der gute Wirkungsgrad erreicht wird, schrumpft. Zusätzlich, da die mechanische Leistung in diesem Bereich mit zunehmender Drehzahl abnimmt, ist die entnehmbare mechanische Leistung geringer.
) sehr schlecht ist; der maximale Wirkungsgrad beträgt nicht mal 50%. Das war Absicht, da sonst der Unterschied zwischen dem linearen und halb-idealen Motor in den Diagrammen kaum sichtbar gewesen wäre. Es ist einsichtig, dass bei einem besseren Motor nicht nur der maximale Wirkungsgrad größer wäre, sondern auch die Drehzahl, bei der dieses Maximum erreicht wird. Anschaulich gesagt wandert der roten Punkt nicht nur nach oben sondern auch nach rechts hin zu größeren Drehzahlen. Ein besserer Wirkungsgrad ist natürlich erwünscht, allerdings läßt sich der Vorteil nicht immer voll nutzen. Zum Einen wird die „Spitze“ der Wirkungsgradkurve spitzer, und der nutzbare Drehzahlbereich, in dem der gute Wirkungsgrad erreicht wird, schrumpft. Zusätzlich, da die mechanische Leistung in diesem Bereich mit zunehmender Drehzahl abnimmt, ist die entnehmbare mechanische Leistung geringer.
Zusammenfassung der wichtigsten Punkte zum Wirkungsgrad
- Der Wirkungsgrad bei der halben Leerlaufdrehzahl, bei der der Motor seine maximale mechanische Leistung liefert, ist immer kleiner als 50%.
- Der maximale Wirkungsgrad wird bei einer Drehzahl zwischen der halben und der vollen Leerlaufdrehzahl erreicht.
- Je größer der Wirkungsgrad ist, ums so kleiner ist der Drehzahlbereich in dem dieser Wirkungsgrad erzielt wird, und um so kleiner ist die nutzbare mechanische Leistung (im Vergleich zur maximalen Leistung).
- Als Faustregel, der optimale Wirkungsgrad wird bei etwa 80-90% der Leerlaufdrehzahl erreicht.
3.3. Leerlauf-Reduktionsfaktor
Der Leerlauf-Reduktionsfaktor ![]() spielt eine entscheidende Rolle. Tatsächlich bestimmt dieser Parameter, bis auf einen Vorfaktor
spielt eine entscheidende Rolle. Tatsächlich bestimmt dieser Parameter, bis auf einen Vorfaktor ![]() , alle Kurvenverläufe vollständig. Auf den Leerlauf-Reduktionsfaktor soll daher noch etwas genauer eingegangen werden. Es wird an Gln. (3.4) und (3.5) erinnert.
, alle Kurvenverläufe vollständig. Auf den Leerlauf-Reduktionsfaktor soll daher noch etwas genauer eingegangen werden. Es wird an Gln. (3.4) und (3.5) erinnert.
Im vorgehenden Beispiel wurde ![]() gewählt, entsprechend einem Motor mit einem maximalen Wirkungsgrad von 47%. Dies macht deutlich, dass
gewählt, entsprechend einem Motor mit einem maximalen Wirkungsgrad von 47%. Dies macht deutlich, dass ![]() im Allgemeinen sehr klein sein wird, im Bereich weniger Prozent, im Einklang mit der natürlichen Erwartung, dass der Leerlaufstrom
im Allgemeinen sehr klein sein wird, im Bereich weniger Prozent, im Einklang mit der natürlichen Erwartung, dass der Leerlaufstrom ![]() für jeden vernünftigen Motor wesentlich kleiner als der Kurzschlusstrom
für jeden vernünftigen Motor wesentlich kleiner als der Kurzschlusstrom ![]() ist. Für gute bürstenlose Motoren kann
ist. Für gute bürstenlose Motoren kann ![]() durchaus kleiner als 1% sein.
durchaus kleiner als 1% sein.
Das bedeutet zum Einen, dass die Leerlaufdrehzahl ![]() nur wenige Prozent kleiner ist als die ideale Leerlaufdrehzahl
nur wenige Prozent kleiner ist als die ideale Leerlaufdrehzahl ![]() , und dass die elektromotorische Konstante
, und dass die elektromotorische Konstante ![]() (bis auf wenige Prozent genau) aus gemessener Leerlaufdrehzahl und Spannung bestimmt werden kann. Andererseits bedeutet dies aber NICHT, dass deswegen auch der Wirkungsgrad sehr groß wäre. Dies liegt an der fatalen Wirkung der Wurzel in den Formeln zum Wirkungsgrad, wie ein einfaches Rechenbeispiel zeigt. Nehmen wir eine Reduktion von 1% an, entsprechend
(bis auf wenige Prozent genau) aus gemessener Leerlaufdrehzahl und Spannung bestimmt werden kann. Andererseits bedeutet dies aber NICHT, dass deswegen auch der Wirkungsgrad sehr groß wäre. Dies liegt an der fatalen Wirkung der Wurzel in den Formeln zum Wirkungsgrad, wie ein einfaches Rechenbeispiel zeigt. Nehmen wir eine Reduktion von 1% an, entsprechend ![]() . Die Leerlaufdrehzahl beträgt dann 99% der idealen Drehzahl, und die maximale gelieferte mechanische Leistung beträgt 98% des Idealfalls. Für die Wurzel ergibt sich aber
. Die Leerlaufdrehzahl beträgt dann 99% der idealen Drehzahl, und die maximale gelieferte mechanische Leistung beträgt 98% des Idealfalls. Für die Wurzel ergibt sich aber ![]() . Die Drehzahl, bei der der maximale Wirkungsgrad erreicht wird, liegt daher bei 91% der Leerlaufdrehzahl, und der maximale Wirkungsgrad selber beträgt gerade einmal 81%.
. Die Drehzahl, bei der der maximale Wirkungsgrad erreicht wird, liegt daher bei 91% der Leerlaufdrehzahl, und der maximale Wirkungsgrad selber beträgt gerade einmal 81%.
| Leerlauf-drehzahl | max. mech. Leistung | Drehzahl max. Wirkungsgrads |
max. Wirkungsgrad |
||
| |
|
|
|
|
|
| 0.5% | 99.5% | 99.0% | 93.4% | 86.4% | 86.8% |
| 1% | 99.0% | 98.0% | 90.9% | 81.0% | 81.8% |
| 2% | 98.0% | 96.0% | 87.6% | 73.7% | 75.2% |
| 5% | 95.0% | 90.2% | 81.7% | 60.3% | 63.5% |
| 10% | 90.0% | 81.0% | 76.0% | 46.7% | 51.9% |
Die vorstehende Tabelle zeigt die Entwicklung relevanter ![]() -Faktoren mit zunehmendem
-Faktoren mit zunehmendem ![]() . Der Bezug zu den obigen Gleichungen ist offensichtlich, bis auf den Faktor in der letzten Spalte, welcher einer Erklärung bedarf.
. Der Bezug zu den obigen Gleichungen ist offensichtlich, bis auf den Faktor in der letzten Spalte, welcher einer Erklärung bedarf.
Der Reduktionsfaktor ![]() hängt mit dem bereits erwähnten Vorfaktor
hängt mit dem bereits erwähnten Vorfaktor ![]() , bzw. genauer mit
, bzw. genauer mit ![]() zusammen. Beide,
zusammen. Beide, ![]() sowie
sowie ![]() , weichen aufgrund des Verlustdrehmoments, beschrieben durch die Parameter
, weichen aufgrund des Verlustdrehmoments, beschrieben durch die Parameter ![]() und
und ![]() im linearen Motormodell, von ihren Idealwerten 1 bzw.
im linearen Motormodell, von ihren Idealwerten 1 bzw. ![]() ab. Im Allgemeinen führt also eine Vergrößerung von
ab. Im Allgemeinen führt also eine Vergrößerung von ![]() implizit auch zu einer Vergößerung von
implizit auch zu einer Vergößerung von ![]() , und umgekehrt. Allerdings geht nur
, und umgekehrt. Allerdings geht nur ![]() in
in ![]() ein. Für den Speziallfall
ein. Für den Speziallfall ![]() bleibt
bleibt ![]() unverändert
unverändert ![]() , und der maximale Wirkungsgrad ist durch den
, und der maximale Wirkungsgrad ist durch den ![]() -Faktor
-Faktor ![]() bestimmt, entsprechend der 5. Spalte. Für den Speziallfall
bestimmt, entsprechend der 5. Spalte. Für den Speziallfall ![]() ergibt sich demgegenüber der Zusammenhang
ergibt sich demgegenüber der Zusammenhang ![]() , und der maximale Wirkungsgrad ist durch
, und der maximale Wirkungsgrad ist durch ![]() gegeben, entsprechend der 6. Spalte. Im Allgemeinen liegt der Wert von
gegeben, entsprechend der 6. Spalte. Im Allgemeinen liegt der Wert von ![]() dazwischen, also
dazwischen, also
![]() , Gl. (3.16)
, Gl. (3.16)
und dementsprechend auch der maximale Wirkungsgrad (dies beeinflusst auch die maximale mechanische Leistung, die Werte in der Tabelle gelten also für ![]() ). Als Nebenbemerkung, es ist also geringfügig besser, wenn die Verluste vorwiegend vom „
). Als Nebenbemerkung, es ist also geringfügig besser, wenn die Verluste vorwiegend vom „![]() -Typ“ sind.
-Typ“ sind.
Die Tabelle liefert im übrigen auch eine Rechtfertigung für die Letzte der oben angegebenen Wirkungsgrad-Faustregeln. Einen Motor mit deutlich mehr als 80% maximalen Wirkungsgrad wird man selten in den Händen halten, andererseits wird man einen Motor mit deutlich weniger als 60% nicht in die Hände nehmen wollen. Dieser Bereich für den Wirkungsgrad (letzten zwei Spalten) übersetzt sich in eine Drehzahl mit maximalen Wirkungsgrad (4. Spalte) von ca 80-90% der Leerlaufdrehzahl.
An dieser Stelle könnte einem eine weitere Merkregel zum Wirkungsgrad auffallen, nämlich, dass der maximale Wirkungsgrad quadratisch mit der Drehzahl an diesem Punkt zusammenhängt. D.h., ist ![]() 10% kleiner als die Leerlaufdrehzahl, ist der maximale Wirkungsgrad um ca. 20% niedriger und beträgt nur noch ca. 80%, bei 15% nur noch etwa 70%, bei 20% nur noch ca. 60%.
10% kleiner als die Leerlaufdrehzahl, ist der maximale Wirkungsgrad um ca. 20% niedriger und beträgt nur noch ca. 80%, bei 15% nur noch etwa 70%, bei 20% nur noch ca. 60%.
Und damit kommen wir zur vielleicht wichtigsten Schlussfolgerung bisher. Nachdem ![]() in der Regel offensichtlich nur wenige Prozent beträgt (vorallem bei brushless Motoren), könnten wir eigentlich in allen Formeln, in denen
in der Regel offensichtlich nur wenige Prozent beträgt (vorallem bei brushless Motoren), könnten wir eigentlich in allen Formeln, in denen ![]() auftaucht, diesen Faktor auch weglassen bzw.
auftaucht, diesen Faktor auch weglassen bzw. ![]() setzen – der Fehler den wir dadurch machen beträgt dann ja auch nur wenige Prozent. Ein Blick nach oben zeigt, dies gilt für alle Formeln, die NICHT mit dem Wirkungsgrad zu tun haben, also für Drehmoment, Leistung, Strom, Drehzahl. Da
setzen – der Fehler den wir dadurch machen beträgt dann ja auch nur wenige Prozent. Ein Blick nach oben zeigt, dies gilt für alle Formeln, die NICHT mit dem Wirkungsgrad zu tun haben, also für Drehmoment, Leistung, Strom, Drehzahl. Da ![]() dem halb-idealen Motor entspricht, heißt dies aber auch, dass wir für alle diese Fragen anstatt des „komplizierten“ Modells genauso gut das einfache halb-ideale Motormodell benutzen können. Oder will irgend jemand behaupten, dass er den KV-Wert seines Motors besser als auf 1% genau kennen würde, oder den Motorwiderstand? Natürlich wäre es genauer mit einem präzisen Motormodell zu arbeiten, aber wenn es um Leistungen, Drehmomente, Ströme und Drehzahlen geht könnte man das auch als Erbsen- äh Prozentzählerei betrachten.
dem halb-idealen Motor entspricht, heißt dies aber auch, dass wir für alle diese Fragen anstatt des „komplizierten“ Modells genauso gut das einfache halb-ideale Motormodell benutzen können. Oder will irgend jemand behaupten, dass er den KV-Wert seines Motors besser als auf 1% genau kennen würde, oder den Motorwiderstand? Natürlich wäre es genauer mit einem präzisen Motormodell zu arbeiten, aber wenn es um Leistungen, Drehmomente, Ströme und Drehzahlen geht könnte man das auch als Erbsen- äh Prozentzählerei betrachten.
Bei Fragen, die den Wirkungsgrad betreffen, dürfen wir den Effekt durch die Verlustdrehmomente aber keinesfalls vernachlässigen. Der halb-ideale Motor liefert die Merkregel ![]() , mehr nicht. Tatsächlich stellt sich bzgl. des Wirkungsgrads die Situation genau gegenteilig wie zuvor dar, wie ein einfaches Rechenbeispiel zeigt. Nehmen wir an wir konnten für unseren Motor den Wert
, mehr nicht. Tatsächlich stellt sich bzgl. des Wirkungsgrads die Situation genau gegenteilig wie zuvor dar, wie ein einfaches Rechenbeispiel zeigt. Nehmen wir an wir konnten für unseren Motor den Wert ![]() mit einer Genauigkeit von 1% bestimmen. Für den Wirkungsgrad bedeutet dies dann einen Fehler von 9%! Der tatsächliche Wirkungsgrad könnte also 85.5% betragen, oder auch nur 77.5%! Einmal wäre man völlig begeistert, das anderemal vielleicht zufrieden. Wer nun weiter sinniert wird feststellen, dass es gar nicht so einfach ist, eine Genauigkeit in
mit einer Genauigkeit von 1% bestimmen. Für den Wirkungsgrad bedeutet dies dann einen Fehler von 9%! Der tatsächliche Wirkungsgrad könnte also 85.5% betragen, oder auch nur 77.5%! Einmal wäre man völlig begeistert, das anderemal vielleicht zufrieden. Wer nun weiter sinniert wird feststellen, dass es gar nicht so einfach ist, eine Genauigkeit in ![]() von 1% zu erreichen. Wenn es also um den Wirkungsgrad geht, reicht ein gutes Motormodell nicht aus, sondern man muss auch ziemlich genau arbeiten um halbswegs vernünftige Aussagen zu erhalten. Tatsächlich, da die Datenbasis bis auf ein paar Ausnahmen sehr dünn ist, könnte man auch zum Schluss kommen, generell alle Aussagen zum Wirkungsgrad, auch die von „Wirkungsgradmessungen“ (welche bis auf sehr wenige Ausnahmen nie wirklich den Wirkungsgrad messen), wenn schon nicht als Hausnummer dann aber mit der allergrößten Vorsicht zu betrachten.
von 1% zu erreichen. Wenn es also um den Wirkungsgrad geht, reicht ein gutes Motormodell nicht aus, sondern man muss auch ziemlich genau arbeiten um halbswegs vernünftige Aussagen zu erhalten. Tatsächlich, da die Datenbasis bis auf ein paar Ausnahmen sehr dünn ist, könnte man auch zum Schluss kommen, generell alle Aussagen zum Wirkungsgrad, auch die von „Wirkungsgradmessungen“ (welche bis auf sehr wenige Ausnahmen nie wirklich den Wirkungsgrad messen), wenn schon nicht als Hausnummer dann aber mit der allergrößten Vorsicht zu betrachten.
Zusammenfassung der wichtigsten Schlussfolgerung zum Motorverhalten und Wirkungsgrad
- Bei allen Fragen, die sich NICHT auf den Wirkungsgrad beziehen, wie die zur Leistung, Drehmoment, Strom, Drehzahl, kann mit im Allgemeinen ausreichender Genauigkeit das Modell des halb-idealen Motors verwendet werden.
- Bestimmungen des Wirkungsgrads bedürfen großer Sorgfalt, und Werte für Wirkungsgrade sollten mit „gesunden Menschenverstand“ bewertet werden.
4. Motorverhalten bei unterschiedlichen Spannungen
„Unterschiedliche“ Spannungen treten bei Helis in verschiedenen Situationen auf. Zum Beispiel als Spannungssteuerung des Motors. Das typische Beispiel ist ein FP-Heli, bei dem Steigen/Senken über die Drehzahl des Rotors und diese wiederrum über die am Motor anliegende Spannung gesteuert wird. Ein anderes Beispiel sind Koaxhelis. Beim CP-Heli taucht die Spannungssteuerung als Gaskurve auf. Eine weitere, anders gelagerte Situation bezieht sich auf die Spannung des Lipos, also z.B. beim 450er auf die Frage, sollen es 3S, 4S, oder gar 6S sein? Alle diese Fälle können über die bereits im vorhergehenden Kapitel erwähnte Kurvenschar im Leistungs-Drehzahl-Diagram ![]() betrachtet werden, wobei für eine Kurve die Spannung konstant ist, aber jede Kurve zu einer anderen Spannung gehört.
betrachtet werden, wobei für eine Kurve die Spannung konstant ist, aber jede Kurve zu einer anderen Spannung gehört.
4.1. Mathematische Beschreibung
Interessanterweise lassen sich die elektromotorischen Konstanten ![]() und
und ![]() , der Motorwiderstand
, der Motorwiderstand ![]() , und die Spannung
, und die Spannung ![]() durch Einführen normierter Betriebsgrößen aus den Motorgleichungen eliminieren. Dies hat tiefgehende Gründe und Implikationen, auf die hier nicht weiter eingegangen werden soll. Für uns genügt es sich bei einigen Größen und Ergebnissen auf die Spannung
durch Einführen normierter Betriebsgrößen aus den Motorgleichungen eliminieren. Dies hat tiefgehende Gründe und Implikationen, auf die hier nicht weiter eingegangen werden soll. Für uns genügt es sich bei einigen Größen und Ergebnissen auf die Spannung ![]() zu beziehen. In Gl. (3.3) wurde das teilweise schon vorweg genommen.
zu beziehen. In Gl. (3.3) wurde das teilweise schon vorweg genommen.
Für die relative Leerlaufspannung ![]() und den relativen Leerlaufstrom
und den relativen Leerlaufstrom ![]() finden wir
finden wir
![]() ,
, ![]() , Gl. (4.1)
, Gl. (4.1)
wobei an ![]() und
und ![]() erinnert wird. Diese „Motorkonstanten“ ändern sich also mit der Spannung (ausser für
erinnert wird. Diese „Motorkonstanten“ ändern sich also mit der Spannung (ausser für ![]() ): Die relative Leerlaufspannung nimmt mit zunehmender Spannung tendenziell zu, der relative Leerlaufstrom ab. D.h., verdoppeln wir die Spannung dann wird die Leerlaufdrehzahl nicht genau doppelt so groß wie zunächst vermutet, sondern wird etwas mehr als doppelt so groß. Entsprechend wird der Leerlaufstrom etwas kleiner als doppelt so groß. Als Folge davon wird der Leerlauf-Reduktionsfaktor
): Die relative Leerlaufspannung nimmt mit zunehmender Spannung tendenziell zu, der relative Leerlaufstrom ab. D.h., verdoppeln wir die Spannung dann wird die Leerlaufdrehzahl nicht genau doppelt so groß wie zunächst vermutet, sondern wird etwas mehr als doppelt so groß. Entsprechend wird der Leerlaufstrom etwas kleiner als doppelt so groß. Als Folge davon wird der Leerlauf-Reduktionsfaktor ![]() tendenziell mit der Spannung kleiner, und damit der maximale Wirkungsgrad größer! Bei höherer Spannung ist die Effizienz des Motors also tendenziell besser (der Effekt ist aber nicht sehr ausgeprägt). Für den Sonderfall
tendenziell mit der Spannung kleiner, und damit der maximale Wirkungsgrad größer! Bei höherer Spannung ist die Effizienz des Motors also tendenziell besser (der Effekt ist aber nicht sehr ausgeprägt). Für den Sonderfall ![]() , der bei Brushlessmotoren gut realisiert sein mag, werden diese Größen von der Spannung unabhängig, und damit „echte“ Motorkonstanten.
, der bei Brushlessmotoren gut realisiert sein mag, werden diese Größen von der Spannung unabhängig, und damit „echte“ Motorkonstanten.
Für die relative mechanische und elektrische Leistung erhält man
![]() , Gl. (4.2)
, Gl. (4.2)
![]() . Gl. (4.3)
. Gl. (4.3)
Was will uns das nun sagen? Nun, in diesen Gleichungen sowie der für den Wirkungsgrad taucht die Drehzahl nur in der Kombination ![]() auf; alle anderen Größen sind spannungsunabhängige Konstanten. D.h., die durch diese Gleichungen beschriebenen Kurven skalieren mit der Spannung
auf; alle anderen Größen sind spannungsunabhängige Konstanten. D.h., die durch diese Gleichungen beschriebenen Kurven skalieren mit der Spannung ![]() ; sie sehen immer gleich aus, nur mal größer und kleiner je nach Spannung!
; sie sehen immer gleich aus, nur mal größer und kleiner je nach Spannung!
Genau genommen wurde die „schwachen“ Spannungsabhängigkeit von ![]() für
für ![]() , wie zuvor diskutiert, hier nicht mit berücksichtigt. Aber auch dann skalieren die Kurven ziemlich gut mit
, wie zuvor diskutiert, hier nicht mit berücksichtigt. Aber auch dann skalieren die Kurven ziemlich gut mit ![]() , und es lohnt nicht diesen Punkt extra zu betrachten (wir betrachten im Folgenden also
, und es lohnt nicht diesen Punkt extra zu betrachten (wir betrachten im Folgenden also ![]() ).
).
4.2. Motordiagramme
Die eben beschriebenen Verhältnisse können wir uns wieder über Motordiagramme veranschaulichen. Ich habe dazu einen Motor mit ![]() und
und ![]() angenommen. Im Gegensatz zu Kapitel 3.2 ist das nun also ein realistischer Fall.
angenommen. Im Gegensatz zu Kapitel 3.2 ist das nun also ein realistischer Fall.
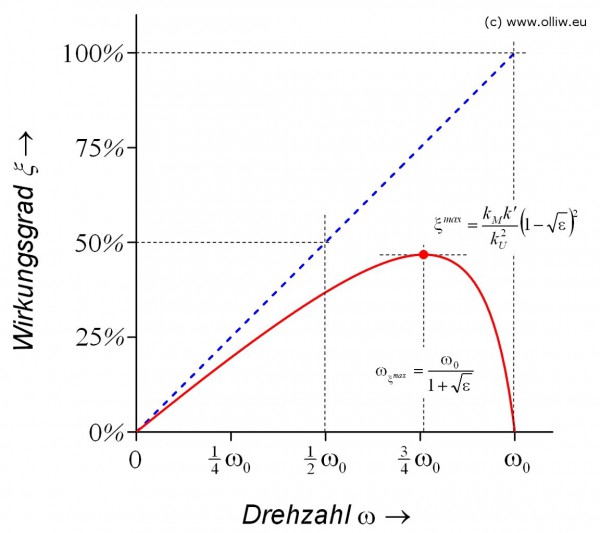
Im nachstehenden Diagram ist die abgegebene mechanische und aufzuwendende elektrische Leistung als Funktion der Drehzahl dargestellt (durchgezogene Linien = ![]() , gestrichelte Linien =
, gestrichelte Linien = ![]() ). Es sind die Kurven für vier Spannungen 1S, 2S, 3S, und 4S gezeichnet.
). Es sind die Kurven für vier Spannungen 1S, 2S, 3S, und 4S gezeichnet.
Entsprechend Gl. (4.1) steigt die Leerlaufdrehzahl proportional mit der Spannung an, ist also bei 4S viermal größer als bei 1S. Die maximale mechanische Leistung nimmt jedoch entsprechend Gl. (4.2) quadratisch mit der Spannung zu. Bei 4S liefert der Motor also 16-mal mehr mechanische Leistung. Ähnlichens gilt für die elektrische Leistung. Eine „Warnung“ jedoch, das eben gesagt bedeutet nicht, dass der Motor diese 16-fache Leistung tatsächlich liefern kann. In den Überlegungen wurde nicht mit berücksichtigt, dass jeder Motor eine maximale thermische Belastung verträgt, d.h., er kann nicht beliebig viel mechanische Leistung liefern. Wird zu viel vom Motor gefordert, überhitzt er. Betrachtet man die Kurven weiter, sieht man das sie alle ziemlich gleich aussehen, nur unterschiedlich „groß“. Das ist es was mit „die Kurven skalieren mit der Spannung ![]() “ gemeint ist, und wie es sich mathematisch in Gln. (4.2) und (4.3) ausdrückt.
“ gemeint ist, und wie es sich mathematisch in Gln. (4.2) und (4.3) ausdrückt.
Betrachten wir nun den Wirkungsgrad; die Kurven für die vier Spannungen sind im nachfolgenden Bild gezeigt.
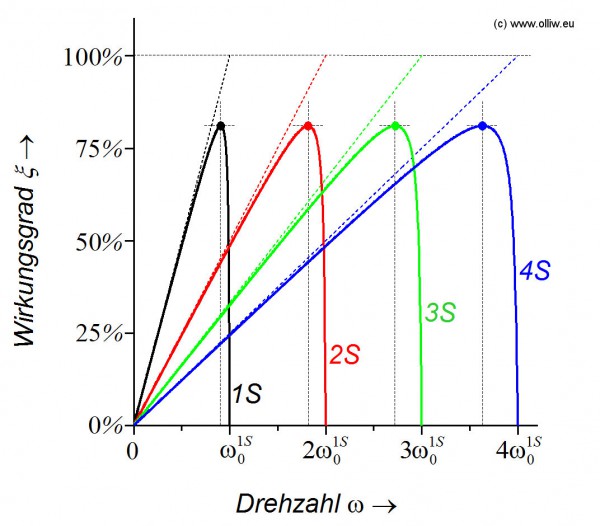
Die Kurven sehen wieder alle sehr ähnlich aus, nur sind sie hier „gestreckt“. Das kommt daher, dass zwar die Leerlaufdrehzahl mit der Spannung zunimmt, aber der Wirkungsgrad sich im Betrag nicht ändert (er kann natürlich nicht z.B. 400% werden!). Für den hier angenommenen Fall ![]() ist der maximale Wirkungsgrad für alle Spannungen gleich groß – bzw. klein, denn er beträgt gerade mal 81.8% trotz des kleinen
ist der maximale Wirkungsgrad für alle Spannungen gleich groß – bzw. klein, denn er beträgt gerade mal 81.8% trotz des kleinen ![]() (siehe Kapitel 3.3). Der maximale Wirkungsgrad wird bei 90.9% der Leerlaufdrehzahl der jeweiligen Spannung erreicht.
(siehe Kapitel 3.3). Der maximale Wirkungsgrad wird bei 90.9% der Leerlaufdrehzahl der jeweiligen Spannung erreicht.
Zusammenfassung der wichtigsten Punkte zum Motorverhalten bei unterschiedlichen Spannungen
- Verdoppeln wir die Spannung dann wird die Leerlaufdrehzahl und der Leerlaufstrom (in etwa) doppelt so groß.
- Verdoppeln wir die Spannung dann wird die mechanische und elektrische Leistung (in etwa) viermal so groß.
- Die Wirkungsgradkurve ändert sich (nahezu) nicht.
5. Motor mit Rotor als Last
Nachdem wir den Motor nun ziemlich genau betrachtet haben, und sich eine handvoll wichtige Merkregeln ergaben, können wir uns endlich der Motor-Rotor-Kombination widmen. Wir stellen uns dazu zunächst vor, dass der Motor direkt mit dem Rotor verbunden ist (zur Ritzel-Frage kommen wir unten). Wie in Kapitel 3 bereits erwähnt, stellt die Last aus der Sicht des Motors ein drehzahlabhängiges Drehmoment dar, bzw., da ich ja lieber die Leistungen betrachte, eine drehzahlabhängige Leistung ![]() .
.
Während uns alle Motor- und Rotoreigenschaften bekannt sind (bzw. bekannt sein müssen), und wir die Spannung ![]() wie zuvor auch vorgeben wollen, sind die Drehzahl
wie zuvor auch vorgeben wollen, sind die Drehzahl ![]() sowie der Strom
sowie der Strom ![]() unbekannt. Eine der beiden Größen müssen wir also mittels der obigen Beziehungen ermitteln; und wir wählen wie zuvor auch die Drehzahl
unbekannt. Eine der beiden Größen müssen wir also mittels der obigen Beziehungen ermitteln; und wir wählen wie zuvor auch die Drehzahl ![]() (der Strom läßt sich dann über Gl. (1.1b) bestimmen). Die Drehzahl mit der sich der Motor und/oder Rotor dreht ergibt sich aus der Forderung, dass der Motor genau das zum Drehen des Rotors benötigte Drehmoment bzw. die entsprechende Leistung liefern muss. Anders gesagt, die Drehzahl ergibt sich aus
(der Strom läßt sich dann über Gl. (1.1b) bestimmen). Die Drehzahl mit der sich der Motor und/oder Rotor dreht ergibt sich aus der Forderung, dass der Motor genau das zum Drehen des Rotors benötigte Drehmoment bzw. die entsprechende Leistung liefern muss. Anders gesagt, die Drehzahl ergibt sich aus
![]() . Gl. (5.1)
. Gl. (5.1)
Nachfolgend werde ich die schwache Spannungsabhängigkeit der relativen Leerlaufdrehzahl bzw. ![]() (siehe Kapitel 4.1) in der Diskussion ignorieren (die Formeln sind jedoch exakt). Dies ist für uns ausreichend genau, vorallem bei brushless Motoren, und verstellt den Blick aufs Wesentliche nicht.
(siehe Kapitel 4.1) in der Diskussion ignorieren (die Formeln sind jedoch exakt). Dies ist für uns ausreichend genau, vorallem bei brushless Motoren, und verstellt den Blick aufs Wesentliche nicht.
5.1. Mathematische Beschreibung
Die Lösung von Gl. (5.1) ergibt sich durch einsetzen von z.B. Gln. (2.3) und (3.6), und wir erhalten:
![]() . Gl. (5.2)
. Gl. (5.2)
Vom Motor müssen wir also nur ![]() und
und ![]() wissen; alle Rotoreigenschaften sind in der Größe
wissen; alle Rotoreigenschaften sind in der Größe ![]() zusammengefasst. Diese Gleichung läßt sich noch etwas „aufhübschen“ zu
zusammengefasst. Diese Gleichung läßt sich noch etwas „aufhübschen“ zu
![]() , Gl. (5.3)
, Gl. (5.3)
wenn wir die Größen ![]() und
und
![]() mit
mit ![]() Gl. (5.4)
Gl. (5.4)
einführen. ![]() gibt die Drehzahl relativ zur Leerlaufdrehzahl an.
gibt die Drehzahl relativ zur Leerlaufdrehzahl an. ![]() enthält alle Eigenschaften des Motor-Rotor-Systems, und ist die entscheidende Kenngröße. Sie gibt an wie „stark“ die Last im Vergleich zur Motorleistung ist:
enthält alle Eigenschaften des Motor-Rotor-Systems, und ist die entscheidende Kenngröße. Sie gibt an wie „stark“ die Last im Vergleich zur Motorleistung ist: ![]() ist die Leistung welche benötigt wird um den Rotor mit der Leerlaufdrehzahl zu drehen, und
ist die Leistung welche benötigt wird um den Rotor mit der Leerlaufdrehzahl zu drehen, und ![]() ist die maximale mechanische Motorleistung. Kleines
ist die maximale mechanische Motorleistung. Kleines ![]() bedeutet also kleine Last, und großes
bedeutet also kleine Last, und großes ![]() eine große Last.
eine große Last.
Gleichung (5.3) läßt sich für ![]() analytisch nach
analytisch nach ![]() auflösen, was Spaß macht und nette Formeln produziert, welche aber wenig nützen. Nützlicher ist es die Grenzfälle
auflösen, was Spaß macht und nette Formeln produziert, welche aber wenig nützen. Nützlicher ist es die Grenzfälle ![]() und
und ![]() zu betrachten (für die Drehzahl erwarten wir dann
zu betrachten (für die Drehzahl erwarten wir dann ![]() bzw.
bzw. ![]() ). Vorallem ist aber interessant wo der Übergang von kleiner zu großer Last liegt, z.B. bei welchem Wert
). Vorallem ist aber interessant wo der Übergang von kleiner zu großer Last liegt, z.B. bei welchem Wert ![]() die Drehzahl genau 50% der Leerlaufdrehzahl (
die Drehzahl genau 50% der Leerlaufdrehzahl (![]() ) ist und der Motor seine maximale Leistung liefert. Wir erhalten
) ist und der Motor seine maximale Leistung liefert. Wir erhalten
| kleine Last |
max. Motorleistung |
große Last |
| |
|
|
Die Ergebnisse sind recht einsichtig. Bei kleiner Last bzw. kleinem Wert von ![]() hat der Motor wenig Arbeit und die Drehzahl ist nur geringfügig kleiner als die Leerlaufdrehzahl. Wird die Last bzw.
hat der Motor wenig Arbeit und die Drehzahl ist nur geringfügig kleiner als die Leerlaufdrehzahl. Wird die Last bzw. ![]() vergrößert, dann hat der Motor mehr zu tun und die Drehzahl verringert sich. In diesem Bereich mit
vergrößert, dann hat der Motor mehr zu tun und die Drehzahl verringert sich. In diesem Bereich mit ![]() arbeitet der Motor mit vernünftigen Wirkungsgrad. Bei einer gewissen Last entsprechend
arbeitet der Motor mit vernünftigen Wirkungsgrad. Bei einer gewissen Last entsprechend ![]() hat sich die Drehzahl auf 50% der Leerlaufdrehzahl erniedrigt und der Motor bietet seine maximale mechanische Leistung auf. Der Wirkungsgrad ist bereits unter 50% gefallen. Wird die Last noch weiter erhöht, so dass
hat sich die Drehzahl auf 50% der Leerlaufdrehzahl erniedrigt und der Motor bietet seine maximale mechanische Leistung auf. Der Wirkungsgrad ist bereits unter 50% gefallen. Wird die Last noch weiter erhöht, so dass ![]() , dann wird der Motor überfordert; die gelieferte mechanische Leistung nimmt ab und der Wirkungsgrad wird sehr schlecht. Der Motor ist im Überlastbereich.
, dann wird der Motor überfordert; die gelieferte mechanische Leistung nimmt ab und der Wirkungsgrad wird sehr schlecht. Der Motor ist im Überlastbereich.
Es ist wichtig zu bemerken, dass ![]() keine Konstante ist. Natürlich hängt
keine Konstante ist. Natürlich hängt ![]() vom Motor, vom Rotordurchmesser usw. ab, aber das ist alles gegeben.
vom Motor, vom Rotordurchmesser usw. ab, aber das ist alles gegeben. ![]() ändert sich aber auch im Flugbetrieb. Bei einem CP-Heli z.B. ändern wir dauernd den Pitch. Größerer Pitch bedeutet eine größere Last für den Motor und damit einen größeren Wert von
ändert sich aber auch im Flugbetrieb. Bei einem CP-Heli z.B. ändern wir dauernd den Pitch. Größerer Pitch bedeutet eine größere Last für den Motor und damit einen größeren Wert von ![]() , und umgekehrt (
, und umgekehrt (![]() wächst mit dem Pitchwinkel, siehe Gl. (2.5)). Bei einem FP-Heli ändern wir dagegen dauernd die Spannung. Für einen Rotor nimmt
wächst mit dem Pitchwinkel, siehe Gl. (2.5)). Bei einem FP-Heli ändern wir dagegen dauernd die Spannung. Für einen Rotor nimmt ![]() (ungefähr proportional) mit der Spannung zu (
(ungefähr proportional) mit der Spannung zu (![]() für
für ![]() , siehe Gl. (5.4)). Bei einem CP-Heli mit Governor finden wir eine Kombination aus Beidem. Hier wird die Spannung je nach Last so geregelt, dass die Drehzahl konstant bleibt, d.h. sowohl
, siehe Gl. (5.4)). Bei einem CP-Heli mit Governor finden wir eine Kombination aus Beidem. Hier wird die Spannung je nach Last so geregelt, dass die Drehzahl konstant bleibt, d.h. sowohl ![]() und
und ![]() ändern sich andauernd in Gl. (5.4).
ändern sich andauernd in Gl. (5.4).
Mit dieser Erkenntnis verstehen wir sofort was bei Pitch- bzw. Spannungsänderung passiert:
Erhöhen wir den Pitch, dann verschiebt sich der Arbeitspunkt zu größerem ![]() und man kommt dem Überlastbereich näher oder tiefer in ihn hinein. Letzteres, also
und man kommt dem Überlastbereich näher oder tiefer in ihn hinein. Letzteres, also ![]() , ist zu vermeiden. Antriebe sind entsprechend auszulegen.
, ist zu vermeiden. Antriebe sind entsprechend auszulegen.
Erhöhen wir die Spannung, dann erhöht sich die Drehzahl, allerdings auch der Wert von ![]() . Das ist interessant. Trotz der bei höherer Spannung größeren verfügbaren Motorleistung rutscht der Betriebspunkt also auch hier in Richtung größere Last, und falls
. Das ist interessant. Trotz der bei höherer Spannung größeren verfügbaren Motorleistung rutscht der Betriebspunkt also auch hier in Richtung größere Last, und falls ![]() überschritten wird gar in den Überlastbereich. Die Gefahr einer Überlastsituation ergibt sich also bei großen Spannungen, und nicht etwa bei kleinen Spannungen, wie man vielleicht vermuten würde!
überschritten wird gar in den Überlastbereich. Die Gefahr einer Überlastsituation ergibt sich also bei großen Spannungen, und nicht etwa bei kleinen Spannungen, wie man vielleicht vermuten würde!
Zusammenfassung zum Motor-Rotorverhalten bei Pitch- und Spannungsänderungen
- Je größer der Pitch desto mehr rutscht das System in Richtung Überlastbereich.
- Je größer die Spannung desto mehr rutscht das System in Richtung Überlastbereich.
Diese Überlegungen gelten unabhängig vom Wert von ![]() (solange
(solange ![]() , was sicher erfüllt ist). D.h. auch wenn die Last, wie bei einem Heli, nicht nur aus dem Rotor besteht, wie in Kapitel 2. diskutiert, gelten diese Trends.
, was sicher erfüllt ist). D.h. auch wenn die Last, wie bei einem Heli, nicht nur aus dem Rotor besteht, wie in Kapitel 2. diskutiert, gelten diese Trends.
Lustigerweise läßt sich Gl. (5.3) für beliebige ![]() analytisch nach der Spannung
analytisch nach der Spannung ![]() auflösen, und die elektrische Leistung als Funktion der Drehzahl kann exakt angegeben werden (die mechanische Leistung ergibt sich trivial aus Gl. (5.1) zu
auflösen, und die elektrische Leistung als Funktion der Drehzahl kann exakt angegeben werden (die mechanische Leistung ergibt sich trivial aus Gl. (5.1) zu ![]() ). Man erhält
). Man erhält
![]() , Gl. (5.5)
, Gl. (5.5)
![]()
![]() . Gl. (5.6)
. Gl. (5.6)
Im Unterschied zu den Gleichungen in den vorhergehenden Kapiteln ist zu bedenken, dass hier ![]() natürlich die Drehzahl des Motor-Rotor-Systems ist, also die sich durch die Belastung mit dem Rotor einstellende Drehzahl. Die Spannung taucht in den Ausdrücken für
natürlich die Drehzahl des Motor-Rotor-Systems ist, also die sich durch die Belastung mit dem Rotor einstellende Drehzahl. Die Spannung taucht in den Ausdrücken für ![]() und
und ![]() nur implizit auf, dahingehend das sich mit zunehmender Spannung natürlich auch die Drehzahl erhöht.
nur implizit auf, dahingehend das sich mit zunehmender Spannung natürlich auch die Drehzahl erhöht.
Diese Gleichungen sind überraschend einfach. In Anbetracht dessen wie viele Parameter benötigt werden um den Motor und den Rotor zu beschreiben, hätte man ein komplizierteres Ergebnis erwarten können. Tatsächlich sind drei Parameter zur Beschreibung des Motor-Rotor-Systems ausreichend, in Gl. (5.6) z.B. ![]() ,
, ![]() und
und ![]() .
.
5.2. Leistungs-Drehzahl-Diagramme
Die Gl. (5.1) läßt sich auch graphisch lösen, indem man den Schnittpunkt der beiden Kurven für ![]() und
und ![]() in einem Leistungs-Drehzahl-Diagramm sucht. Mit solchen Diagrammen lassen sich auch die eben beschriebenen Zusamenhänge veranschaulichen.
in einem Leistungs-Drehzahl-Diagramm sucht. Mit solchen Diagrammen lassen sich auch die eben beschriebenen Zusamenhänge veranschaulichen.
Im nachfolgenden Diagramm ist die Leistungskurve eines Motors mit ![]() und
und ![]() in rot gezeigt. Die dunkelgrünen Kurven zeigen die Lastkurven für drei verschiedene Rotoren (
in rot gezeigt. Die dunkelgrünen Kurven zeigen die Lastkurven für drei verschiedene Rotoren (![]() ). Bei Kurve
). Bei Kurve  stellt der Rotor eine starke Last dar, bei Kurve
stellt der Rotor eine starke Last dar, bei Kurve 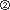 liegt der Rotor genau an der Grenze
liegt der Rotor genau an der Grenze ![]() , und bei Kurve
, und bei Kurve  ist der Rotor eine schwache Last.
ist der Rotor eine schwache Last.
Die sich einstellende Drehzahl ergibt sich aus dem Schnittpunkt der Motor- und Rotorkurve, wie im Bild durch Punkte und gestrichelte Linien markiert. Es ist sofort zu erkennen, dass sich die Drehzahl mit zunehmender Last erniedrigt. Mit zunehmender Last steilt sich die Lastkurve immer mehr auf (Kurven 
![]()
![]()
 ), und der Schnittpunkt wandert im Diagram nach links. Zusätzlich ist für die drei Betriebspunkte der Motorwirkungsgrad angegeben. Bei Rotor
), und der Schnittpunkt wandert im Diagram nach links. Zusätzlich ist für die drei Betriebspunkte der Motorwirkungsgrad angegeben. Bei Rotor  arbeitet der Motor mit maximalen Wirkungsgrad. Generell arbeitet der Motor in diesem Lastbereich am effizientesten. Bei Rotor
arbeitet der Motor mit maximalen Wirkungsgrad. Generell arbeitet der Motor in diesem Lastbereich am effizientesten. Bei Rotor  liefert der Motor seine maximale Leistung, dementsprechend ist der Wirkungsgrad kleiner als 50%. Bei Rotor
liefert der Motor seine maximale Leistung, dementsprechend ist der Wirkungsgrad kleiner als 50%. Bei Rotor  ist der Motor überlastet, zu erkennen am sehr schlechten Wirkungsgrad. Die Kurven
ist der Motor überlastet, zu erkennen am sehr schlechten Wirkungsgrad. Die Kurven 
![]()
![]()
 können auch als die Lastkurven für einen Rotor mit zunehmenden Pitch betrachtet werden.
können auch als die Lastkurven für einen Rotor mit zunehmenden Pitch betrachtet werden.
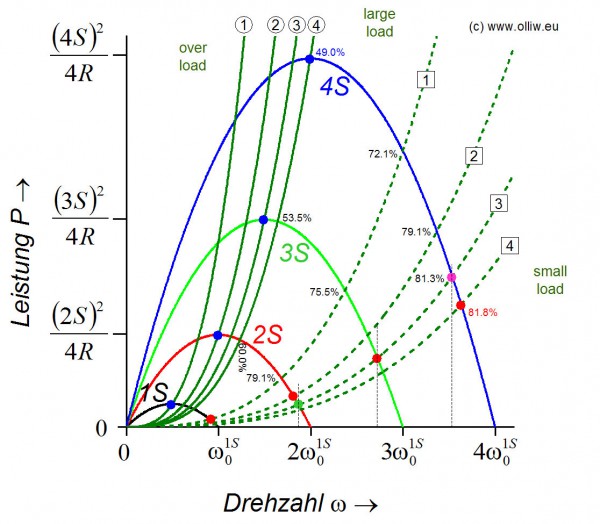
In ähnlicher Weise kann der Effekt unterschiedlicher Motorspannungen diskutiert werden. Dazu tragen wir wie in Kapitel 4.2. die Motorleistungskurven für unterschiedliche Spannungen in das Leistungs-Drehzahl-Diagram ein. Im nächsten Bild sind sie für die vier Spannungen 1S, 2S, 3S, und 4S für den selben Motor wie eben (und in Kapitel 4.2) gezeigt. Zusätzlich sind die Leistungskurven für acht verschiedene Rotoren eingezeichnet. Die sich einstellende Drehzahl ergibt sich wie zuvor aus den Schnittpunkten der ![]() und
und ![]() Kurven, welche für einige Fälle durch Punkte markiert sind. Die acht Rotoren wurden nicht zufällig gewählt: Bei Rotor
Kurven, welche für einige Fälle durch Punkte markiert sind. Die acht Rotoren wurden nicht zufällig gewählt: Bei Rotor  (durchgezogene Kurve
(durchgezogene Kurve  ) gibt der Motor bei 1S gerade seine maximale Leistung ab, bei Rotor
) gibt der Motor bei 1S gerade seine maximale Leistung ab, bei Rotor  bei 2S, bei Rotor
bei 2S, bei Rotor  bei 3S und bei Rotor
bei 3S und bei Rotor  bei 4S (Schnittpunkt im Maximum der Glockenkurve, blaue Punkte). Bei Rotor
bei 4S (Schnittpunkt im Maximum der Glockenkurve, blaue Punkte). Bei Rotor  (gestrichelte Kurve
(gestrichelte Kurve  ) arbeitet der Motor gerade bei 1S mit seiner maximalen Effizienz, bei Rotor
) arbeitet der Motor gerade bei 1S mit seiner maximalen Effizienz, bei Rotor  bei 2S, bei Rotor
bei 2S, bei Rotor  bei 3S und bei Rotor
bei 3S und bei Rotor  bei 4S (rote Schnittpunkte). Für einige Fälle ist der Wirkungsgrad angeschrieben.
bei 4S (rote Schnittpunkte). Für einige Fälle ist der Wirkungsgrad angeschrieben.
Es läßt sich sofort ablesen, dass mit zunehmender Spannung die Drehzahl ansteigt, wie wir es natürlich erwarten. Das ist für Kurve  exemplarisch gezeigt: Der Schnittpunkt mit den Motor-Glockenkurven verschiebt sich zu höheren Drehzahlen, wie für die Spannungen 2S, 3S, und 4S durch den grünen, roten, und pinken Punkt angedeutet. Es lässt sich auch erkennen, dass der Motor mit zunehmender Spannung eher überlastet wird, wie in Kapitel 4.1 betont. Dies deutet sich z.B. dadurch an, dass der Wirkungsgrad bei höheren Spannungen kleiner wird, wie z.B. bei Rotor
exemplarisch gezeigt: Der Schnittpunkt mit den Motor-Glockenkurven verschiebt sich zu höheren Drehzahlen, wie für die Spannungen 2S, 3S, und 4S durch den grünen, roten, und pinken Punkt angedeutet. Es lässt sich auch erkennen, dass der Motor mit zunehmender Spannung eher überlastet wird, wie in Kapitel 4.1 betont. Dies deutet sich z.B. dadurch an, dass der Wirkungsgrad bei höheren Spannungen kleiner wird, wie z.B. bei Rotor  , wo er von 79.1% bei 2S auf 72.1% bei 4S sinkt. Drastischer ist die Situation bei den Rotoren
, wo er von 79.1% bei 2S auf 72.1% bei 4S sinkt. Drastischer ist die Situation bei den Rotoren  bis
bis  . Beim Rotor
. Beim Rotor  sinkt der Wirkungsgrad von vielleicht noch akzeptablen 60% bei 2S auf 49% bei 4S. Bei den Rotoren
sinkt der Wirkungsgrad von vielleicht noch akzeptablen 60% bei 2S auf 49% bei 4S. Bei den Rotoren  ,
,  , und
, und  kommt der Motor bei hohen Spannungen sogar in den Überlastbereich (Schnittpunkt links vom Maximum der Motor-Glockenkurve).
kommt der Motor bei hohen Spannungen sogar in den Überlastbereich (Schnittpunkt links vom Maximum der Motor-Glockenkurve).
5.3. Getriebe und Ritzelgröße
Für einen gegebenen Rotor und gegebenen Motor kann es passieren, dass der Motor zwar eigentlich über ausreichend Leistung verfügt um den Rotor mit der gewünschten Drehzahl anzutreiben, aber der Motor trotzdem z.B. überlastet wird. Ein Beispiel ist Kurve  im vorletzten Bild, bei der sich der Schnittpunkt links des Maximums der Motor-Glockenkurve befindet. Die maximale mechanische Leistung des Motors ist offensichtlich ausreichend, allerdings liegt der Betriebspunkt so ungünstig, dass der Motor ineffizient arbeitet. Ein Getriebe ist hier die Lösung.
im vorletzten Bild, bei der sich der Schnittpunkt links des Maximums der Motor-Glockenkurve befindet. Die maximale mechanische Leistung des Motors ist offensichtlich ausreichend, allerdings liegt der Betriebspunkt so ungünstig, dass der Motor ineffizient arbeitet. Ein Getriebe ist hier die Lösung.
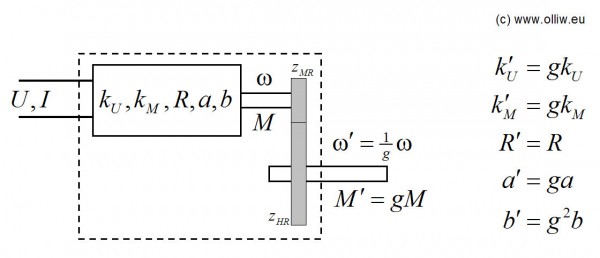
Mit einem Getriebe wird, klaro, die Drehzahl des Motors an die Drehzahl des Rotors angepasst. Die Auswirkung eines Getriebes kann man sich unterschiedlich verdeutlichen, z.B. dadurch, dass man sich den Motor und das Getriebe als eine Einheit vorstellt, wie im nachfolgenden Bild skizziert. Die Motor-Getriebe-Einheit betrachten wir also quasi als einen „neuen“ Motor, welchen wir als „Getriebemotor“ bezeichnen wollen. Der Einfachheit halber werde ich den Getriebemotor meistens einfach „Motor“ nennen.
Durch das Getriebe, mit dem Übersetzungsverhältnis ![]() , verringert sich natürlich die Drehzahl im Verhältnis
, verringert sich natürlich die Drehzahl im Verhältnis ![]() , da der Getriebemotor aber die gleiche Leistung wie der ursprüngliche Motor liefert, erhöht sich das verfügbare Drehmoment dementsprechend um
, da der Getriebemotor aber die gleiche Leistung wie der ursprüngliche Motor liefert, erhöht sich das verfügbare Drehmoment dementsprechend um ![]() . Dieser Sachverhalt lässt sich auch so darstellen, dass dem Getriebemotor „neue“ Motorparameter zugeschrieben werden, welche sich wie im Bild angegeben aus den ursprünglichen Motorparametern ergeben (die „gestrichenen“ Größen beziehen sich auf den Getriebemotor, die „ungestrichenen“ Größen auf den Motor ohne Getriebe). Für die maximale mechanische Motorleistung und den Rotor-Motor-Parameter
. Dieser Sachverhalt lässt sich auch so darstellen, dass dem Getriebemotor „neue“ Motorparameter zugeschrieben werden, welche sich wie im Bild angegeben aus den ursprünglichen Motorparametern ergeben (die „gestrichenen“ Größen beziehen sich auf den Getriebemotor, die „ungestrichenen“ Größen auf den Motor ohne Getriebe). Für die maximale mechanische Motorleistung und den Rotor-Motor-Parameter ![]() bzw.
bzw. ![]() ergibt sich
ergibt sich ![]() und
und ![]() (und analog für
(und analog für ![]() ).
).
Die Getriebeverluste (typisch 5%) haben wir bisher noch nicht bedacht. Diese können mit berücksichtigt werden, indem die Verlustparameter ![]() und
und ![]() angepasst werden, z.B. als
angepasst werden, z.B. als ![]() und
und ![]() . Die Getriebeverluste sollen uns im Folgenden jedoch nicht weiter interessieren. Wir stehen ja selten vor der Frage, Getriebe ja oder nein, sondern davor welches Übersetzungsverhältnis zu wählen ist, und die Getriebeverluste ändern sich nur leicht bei geringfügig unterschiedlichen Übersetzungsverhätlnissen.
. Die Getriebeverluste sollen uns im Folgenden jedoch nicht weiter interessieren. Wir stehen ja selten vor der Frage, Getriebe ja oder nein, sondern davor welches Übersetzungsverhältnis zu wählen ist, und die Getriebeverluste ändern sich nur leicht bei geringfügig unterschiedlichen Übersetzungsverhätlnissen.
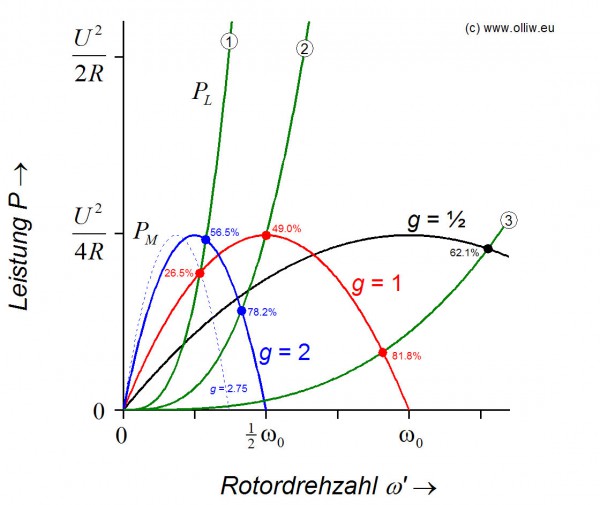
Die verfügbare mechanische Leistung ändert sich also durch das Getriebeverhältnis (praktisch) nicht, allerdings die Rotordrehzahl ![]() . D.h., in einem Leistungs-Drehzahl-Diagram wird die Motor-Glockenkurve entsprechend der Getriebeübersetzung
. D.h., in einem Leistungs-Drehzahl-Diagram wird die Motor-Glockenkurve entsprechend der Getriebeübersetzung ![]() horizontal gestaucht (falls
horizontal gestaucht (falls ![]() ) oder gestreckt (falls
) oder gestreckt (falls ![]() ). Dies ist im nächsten Bild für den selben Motor und die selben Rotoren wie im ersten Bild von Kapitel 5.2 gezeigt.
). Dies ist im nächsten Bild für den selben Motor und die selben Rotoren wie im ersten Bild von Kapitel 5.2 gezeigt.
Betrachten wir zunächst Rotor  . Mit diesem Rotor wird der Motor ohne Getriebe (
. Mit diesem Rotor wird der Motor ohne Getriebe (![]() , rote Kurve) überlastet; der Schnittpunkt ist links vom Maximum der Motor-Glockenkurve und der Wirkungsgrad 26.5%. Mit einem Getriebe lässt sich die Motor-Glockenkurve stauchen, und das Maximum nach links verschieben. Dementsprechend ist es durch geeignete Wahl des Getriebes möglich, einen Schnittpunkt rechts des Maximums der Glockenkurve zu erhalten. Dies ist für ein
, rote Kurve) überlastet; der Schnittpunkt ist links vom Maximum der Motor-Glockenkurve und der Wirkungsgrad 26.5%. Mit einem Getriebe lässt sich die Motor-Glockenkurve stauchen, und das Maximum nach links verschieben. Dementsprechend ist es durch geeignete Wahl des Getriebes möglich, einen Schnittpunkt rechts des Maximums der Glockenkurve zu erhalten. Dies ist für ein ![]() Getriebe im Bild gezeigt (blaue Kurve). Der Wirkungsgrad erhöht sich auf 56.5%, bei sogar etwas höherer Drehzahl des Rotors. Wollte man die selbe Drehzahl wie zuvor erreichen, müsste man in diesem Fall
Getriebe im Bild gezeigt (blaue Kurve). Der Wirkungsgrad erhöht sich auf 56.5%, bei sogar etwas höherer Drehzahl des Rotors. Wollte man die selbe Drehzahl wie zuvor erreichen, müsste man in diesem Fall ![]() noch etwas größer wählen (und die Glockenkurve noch mehr stauchen). Mit
noch etwas größer wählen (und die Glockenkurve noch mehr stauchen). Mit ![]() ergibt sich genau die selbe Drehzahl, bei einem Wirkungsgrad von 74%. D.h. mit einem Getriebe lässt sich hier, bei gleicher Rotordrehzahl bzw. gleichem Schub, der Wirkungsgrad von 26.5% auf 74% verbessern (Getriebeverluste nicht berücksichtigt).
ergibt sich genau die selbe Drehzahl, bei einem Wirkungsgrad von 74%. D.h. mit einem Getriebe lässt sich hier, bei gleicher Rotordrehzahl bzw. gleichem Schub, der Wirkungsgrad von 26.5% auf 74% verbessern (Getriebeverluste nicht berücksichtigt).
Interessant ist auch die Situation für Rotor 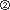 . Ohne Getriebe arbeitet der Motor mit maximaler Leistung; der Schnittpunkt liegt auf dem Maximum der Glockenkurve. Würde die Glockenkurve mittels eines Getriebes gestaucht oder gestreckt, würde sich in jedem Fall eine niedrigere Rotordrehzahl einstellen, und weniger Schub erzeugt werden, da der Motor notwendigerweise weniger als seine maximale Leistung liefern würde. Will man hier bei gleicher Drehzahl einen besseren Wirkungsgrad erzielen, bleibt nichts anderes übrig, als einen Motor mit größerer Leistung zu verwenden.
. Ohne Getriebe arbeitet der Motor mit maximaler Leistung; der Schnittpunkt liegt auf dem Maximum der Glockenkurve. Würde die Glockenkurve mittels eines Getriebes gestaucht oder gestreckt, würde sich in jedem Fall eine niedrigere Rotordrehzahl einstellen, und weniger Schub erzeugt werden, da der Motor notwendigerweise weniger als seine maximale Leistung liefern würde. Will man hier bei gleicher Drehzahl einen besseren Wirkungsgrad erzielen, bleibt nichts anderes übrig, als einen Motor mit größerer Leistung zu verwenden.
Im Falle von Rotor  arbeitet der Motor ohne Getriebe mit maximalen Wirkungsgrad (81.8%), d.h. der Motor ist perfekt an den Rotor angepasst. Ist man jedoch bereit, einen niedrigeren Wirkungsgrad in Kauf zu nehmen, dann lässt sich aus dem selben Motor mehr Leistung heraus quetschen. Mit einem
arbeitet der Motor ohne Getriebe mit maximalen Wirkungsgrad (81.8%), d.h. der Motor ist perfekt an den Rotor angepasst. Ist man jedoch bereit, einen niedrigeren Wirkungsgrad in Kauf zu nehmen, dann lässt sich aus dem selben Motor mehr Leistung heraus quetschen. Mit einem ![]() Getriebe (schwarze Kurve) würde man die 2,7-fache Leistung bei einem Wirkungsgrad von 62% erhalten.
Getriebe (schwarze Kurve) würde man die 2,7-fache Leistung bei einem Wirkungsgrad von 62% erhalten.
Wir können nun die praxisrelevante Frage nach dem passenden Motorritzel betrachten. Wir gehen also davon aus, dass, wie üblich, die Zähnezahl des Hauptzahnrads durchs Modell vorgegeben ist. Das Getriebeverhältnis ergibt sich dann zu ![]() , wobei
, wobei ![]() die Zähnezahl des Motorritzels und
die Zähnezahl des Motorritzels und ![]() die des Hauptzahnrads ist. Für einen gegebenen Motor und gegebenem Rotor, gegebener Spannung und gegebenem Hauptzahnrad, wie hängt dann die Rotordrehzahl
die des Hauptzahnrads ist. Für einen gegebenen Motor und gegebenem Rotor, gegebener Spannung und gegebenem Hauptzahnrad, wie hängt dann die Rotordrehzahl ![]() vom Motoritzel
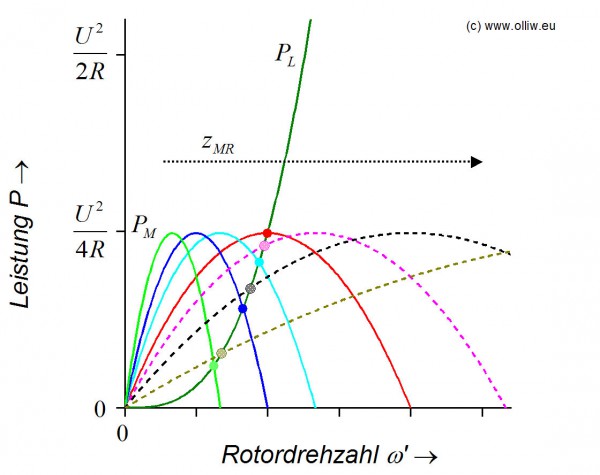
vom Motoritzel ![]() ab? Die Antwort zeigt das nachfolgende Bild.
ab? Die Antwort zeigt das nachfolgende Bild.
Mit zunehmender Zähnezahl des Motorritzels wandert die Motorglockenkurve im Leistungs-Drehzahl-Diagram von links nach rechts. D.h. der Schnittpunkt mit der Rotorlastkurve wird zunächst entlang dieser nach oben wandern und die Rotordrehzahl wird ansteigen, solange bis der Punkt erreicht ist an dem der Motor die maximale Leistung liefert (durchgezogene Kurven und ausgemalte Punkte). Mit weiter zunehmender Zähnezahl wird sich die Drehzahl wieder verringern, und der Motor wird überlastet (gestrichelte Kurven und karrierte Punkte). Im Prinzip können wir also durch Ausprobieren verschiedener Ritzel und Beobachten der Rotordrehzahl den Punkt finden, bei dem der Motor seine maximale Leistung liefert bzw. an dem der Übergang vom Normal- in den Überlastbereich stattfindet, ohne jegwegliche weitere Informationen zum Motor-Rotor-System, wie die verschiedenen Parameter, wissen zu müssen.
Fortsetzung folgt

1 Kommentare